區塊鏈:如何利用門限簽名來生成隨機信標？

編者按：本文來自：以太坊愛好者，作者：ALEXANDERSKIDANOV，翻譯&校對:IANLIU&阿劍，Odaily星球日報經授權轉載。

回顧2015，DFinity項目提出了令整個社區都為之興奮的隨機信標方案——使用BLS門限簽名產生隨機輸出，同時保證輸出的無偏性及不可預測性。然而，時至2020年的今天，構建無偏且不可預測的隨機信標仍然困難重重，還在研究的項目少之又少。其實門限簽名只是構建隨機信標的可行方法之一，我們前面發表過一篇概覽文章，介紹其他可能的解決方法，其中包含本文要重點提到的一種。其他細節——隨機信標是什么？什么是無偏性及不可預測性？除了門限簽名還有什么方法——這些問題都能在上述概覽中得到解答。經過了多次設計迭代，我們最終提出類似DFinity的方案，這也是我們進一步深入理解隨機信標的大好契機。本文將以淺顯的形式，講述門限簽名生成隨機數的一系列協議。密碼學基礎知識

為了更好地了解本文中提到的隨機信標，我們需要掌握一些基礎密碼學知識。首先，我們必須區分兩個概念：1.在本文中以小寫字母表示標量，或者說普通常量；2.用大寫字母表示橢圓曲線上的點。我們不需要對橢圓曲線點了解得很透徹，只要掌握下面兩點：橢圓曲線點可以相加，也可以跟標量相乘，然后得到另一個橢圓曲線點。即使知道G和xG的值，也不可能計算出x的值。在本文中，我們還將用到k-1階多項式p(x)；關于p(x），你不用想太多，只要把它當成一個方程就好，而且：只要你知道在k個不同的x下p(x)的值，你就能推導出所有x的p(x)值。以此類推，對于同一個函數p(x)和基點G，如果你知道p(x)G代入k個不同的x值后的值，就可以推導出所有x所對應的p(x)G值。只要明白了有關橢圓曲線點的這些屬性，就能深度理解隨機信標的工作原理了。隨機信標

直播 ｜ 玉竹 > 經濟下行時如何踩到新浪潮:金色財經 · 直播主辦的《 幣圈 “后浪” 仙女直播周》第4期今晚20:00準時開始，本期“后浪”仙女區塊鏈行業資深從業者玉竹將在直播間聊聊 “合經濟下行時如何踩到新浪潮？”，感興趣的朋友掃碼移步收聽！[2020/6/8]

假設1：系統中有n個參與者，至少需要其中的k位才能產生隨機數。就算控制其中的k-1人，你也不能預知隨機信標的輸出結果、無法操縱結果。

假設2：現在有個k-1階多項式p(x)，參與者1知道p(1)的值、參與者2知道p(2)的值、……、參與者n知道p(n)的值；大家約好使用G作為橢圓曲線基點，所有參與者都知道p(x)G代入所有x的值。我們將p(i)視為參與者i的“私人份額”，而p(i)G是其“公開份額”要設計好的隨機信標，最困難的部分，就是要找到這么一個多項式，使得每個參與者都能知道自己的私人份額，但是無法知道他人的私人份額——這也被稱為分布式密鑰生成。DKG會放在下個章節討論，現在就先假設存在這么個多項式，而所有人都知道各自的私人份額。我們接著討論，如何使用這套假設在區塊鏈協議中產生一個隨機信標？假設網絡產生一個區塊，區塊哈希為h。現在參與者們想用h作為種子以生成隨機數，首先用約定好的函數，將h轉換為某條橢圓曲線上的一個點：H=scalarToPoint(h)對于參與者i來說，因為他知道p(i)和H，所以可以自行計算出H_i=p(i)H。對外公布H_i并不會導致參與者i的私人份額p(i)暴露，因此在每個區塊中都能重用同樣的私人份額，因此DKG只需要進行一次。根據前面提到的第三點特性，當至少有k位參與者公布他們各自的H_i=p(i)H之后，其他人就能知道代入任何一個x之后，H_x=p(x)H是什么。然后所有參與者都可以在自己本地計算H_0=p(0)H，并以這個結果的哈希值作為隨機信標的輸出；請注意，因為沒有參與者知道p(0)，所以唯一能得到p(0)H的方法就是對p(x)H進行內插法計算，要完成內插計算需要知道至少k個p(i)H的值。如果公布的人不足k位，則其他人無法推出p(0)H的值。

聲音 | 中國市場學會理事張銳：無論Libra命運如何 Facebook都是大贏家:7月18日，中國市場學會理事、經濟學教授張銳發表文章《無論Libra命運如何，Facebook都是大贏家》。文章指出，由于Libra錨定了銀行存款、政府債券以及一籃子貨幣，完全可以量度商品的價值，同時可以充當商品交換的媒介，并作為標的進入公眾財富的儲藏范疇。因此，即便是Libra不能獲得全球性法定貨幣的身份，但它完全能夠以數字貨幣的身份像比特幣那樣在商品與服務流通領域長袖善舞，而且龐大的用戶群體為其創造的價值空間一定比任何一種數字貨幣要廣闊寬泛得多。不僅如此，Libra還可像微信和支付寶那樣打開數字金融與數字社會的入口，從而將Facebook帶入新的商業模式。[2019/7/18]

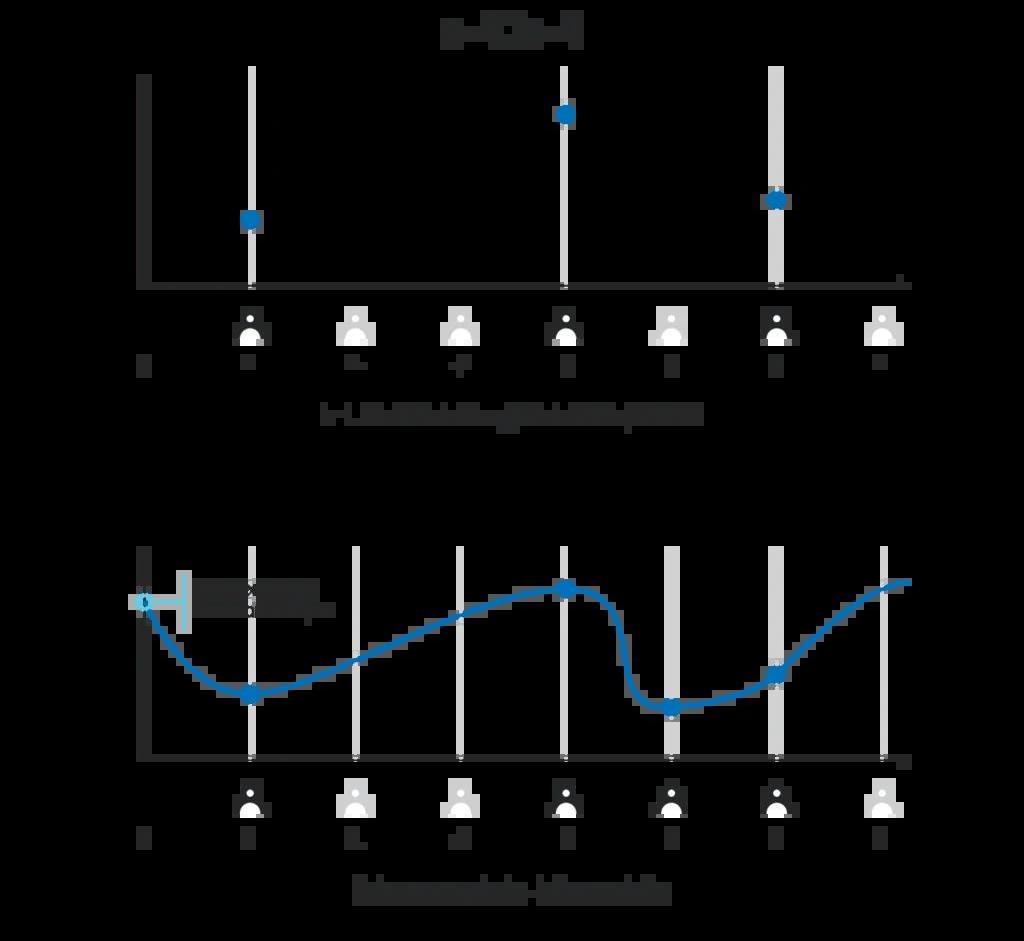
基于此技術構建的信標延續了這些我們所需的特性：如果攻擊者只掌控了少于k-1位參與者，則他無法操控隨機信標的輸出；其他k位參與者才能計算出最終輸出，他們的子集或其他更多的參與者，都能得出相同的輸出。我們還忽略了一件事。為了使用插值法計算p(0)H，必須保證參與者i所公開的H_i真的等于p(i)H。但是因為除了參與者i，其他參與者都不知道p(i)是什么，所以沒法直接驗證參與者i公布的H_i是否的確等于p(i)H；如果不要求為H_i附上密碼學證明，攻擊者可以直接聲稱某個H_i的值，而其他人沒有辦法辨別真偽。

聲音 | 推特CEO：推特正在“考慮”如何應用區塊鏈技術:據coindesk報道，推特CEO Jack Dorsey今日向美國國會委員會表示，該社交媒體公司正在為其平臺探索區塊鏈解決方案。Dorsey表示，區塊鏈具有很多未開發的潛力，特別是圍繞分布式信任和分布式執行。推特目前沒有在區塊鏈上研究得那么深入，但Dorsey愿意了解應怎樣把區塊鏈應用到推特，該公司現在確實有員工在“考慮”此事。[2018/9/6]

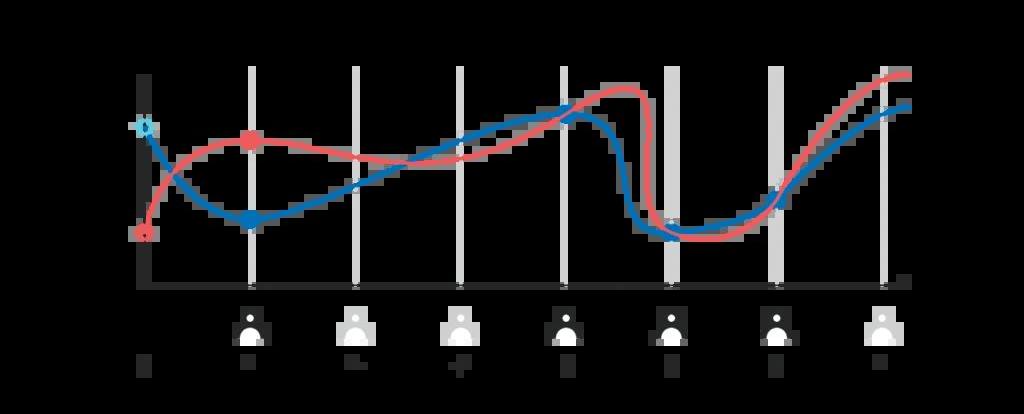
有至少兩種密碼學證明辦法，可以用來判別H_i的真偽。我們會在聊完DKG之后介紹。分布式密鑰生成

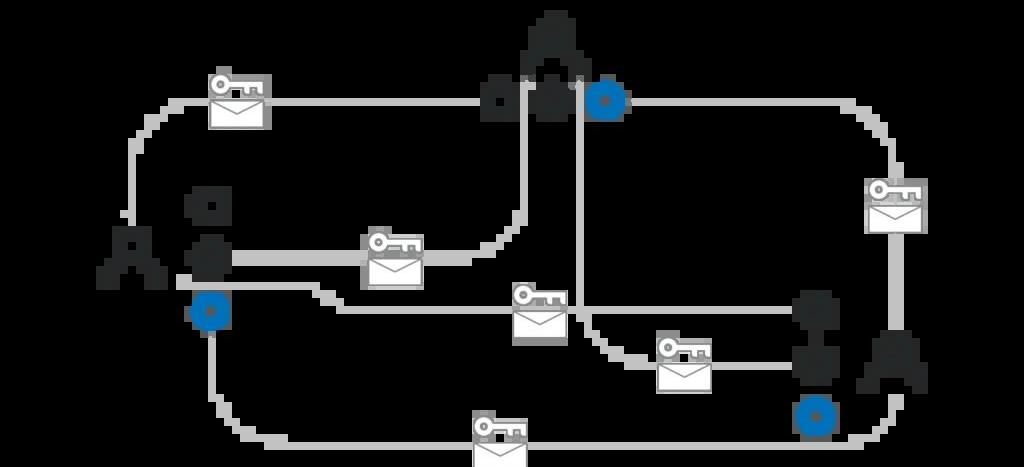
根據前面章節對隨機信標的介紹，我們需要n位參與者共同使用某個k-1階多項式p(x)，使得每個參與者i知道自己的p(i)，而其他人無法得知。下一步，需要所有參與者都知道：給定G時，所有的x所對應的p(x)g值。在本章節，我們假設每個人都有自己的私鑰x_i，而且其他人都知道x_i對應的公鑰X_i。那么運行DKG的一種方式如下：

布魯金斯學會：全球監管機構之間沒有就如何處理加密貨幣達成協議:據福布斯消息，布魯金斯學會昨日發布關于央行和加密貨幣的研究報告。報告指出，世界各地的銀行監管機構并未采取統一的方式來規范加密貨幣。該報告還指出，目前的大型經濟體中，沒有任何一個國家的央行認真考慮是否推出自己的加密貨幣。然而，美聯儲、日本央行、加拿大央行、英國央行和歐洲央行均表示正在評估央行加密貨幣的利與弊。研究表明，央行領導人目前主要對于加密貨幣潛在的逃稅和洗錢可能表示擔心。[2018/4/18]

每個參與者i在本地運行k-1階多項式p_i(x)的計算。接著用公鑰X_j將每個p_i(j)加密，并發送給對應的參與者j。如此一來，只有參與者j能解密出p_i(j)；參與者i還要公布所有p_i(j)G，j∈1~k。所有參與者要對一個至少由k個多項式組成的集合達成共識。因為有些參與者可能掉線，所以他們不可能等到n個驗證者都作出如此承諾再進行下一步；只要至少k個驗證者都作出“收到至少k個這樣的多項式”的承諾之后，他們就可以使用某種形式的共識算法對他們所收到多項式的子集Z達成共識。所有參與者共同驗證加密的p_i(j)與公開的p_i(j)G是否對應，并從Z中移除不合格的多項式。對于集合Z中的每個多項式p_i(x)，每個參與者j自行計算p_i(j)的總和作為私人份額p(j)；同樣的，對于集合Z中的每個p_i(x)G，參與者可以計算p_i(x)G的總和作為公開份額p(x)G。

中國紀檢監察報：中國區塊鏈發展的最大挑戰是“如何讓監管理解區塊鏈并適度監管”: 中國紀檢監察報發文表示，區塊鏈底層技術獲得實質性突破之前的這個階段，恰恰是一個戰略機遇期。如果中國區塊鏈行業能緊密合作，監管能夠適當包容、鼓勵，中國在區塊鏈領域引領全球指日可待。實際上，區塊鏈技術最終必然演化為“監管融入技術”的模式，區塊鏈的難以篡改、共享賬本和分布式的特性，更易于監管介入，獲得更加全面實時的監管數據。讓監管機構本身也參與到技術中去，通過技術本身實現對技術的監管，最終化解區塊鏈與監管的沖突。[2018/3/6]

因為p(x)是每個獨立的p_i(x)的總和，每個p_i(x)都是k-1階多項式，所以要觀察p(x)是否也是k-1階多項式。其次要注意，每個參與者j只知道p(j)的值，但不知道其他p(x)的值。實際上，為了知道p(x）的值，TA需要知道所有的p_i(x），只要至少一個被承諾多項式的值屬于未知，TA就不可能知道p(x)。上述步驟組成了完整的DKG過程。步驟1、2、4相對直觀，但第3步就比較復雜了。具體來解釋第三步——我們需要找個方法，證明每個加密的p_i(j)與公開的p_i(j)G存在對應關系。如果沒有這種驗證，攻擊者i可以向參與者j胡亂發送消息，而不是發送正確的加密p_i(j)，導致參與者j無法進一步計算自己的私人份額。雖然有辦法可以制作出加密份額的形式正確性密碼學證明。但是，這樣的證明數據過大，并且要向全網公布這樣的證明，時間復雜度可能高達O(nk)，證明的size是嚴重的瓶頸。在NEAR協議中，我們不去證明p_i(j)與公開的p_i(j)G的關系，而是在DKG過程中給予每個參與者充分的時間，去證明“他們收到的p_i(j)與公開廣播的p_i(j)G對不上”。協議中假設每個參與者在窗口期內至少會上線一次，而他們提交的挑戰就能進入區塊鏈。對于區塊生產者來說，這兩個假設都很合理，因為要做區塊生產者，一般來說在整個epoch中都要在線；如果大多數區塊生產者密謀不接收這條消息，其實整個系統就已經不安全，攻擊者其實有更好的方式攻擊整個系統。

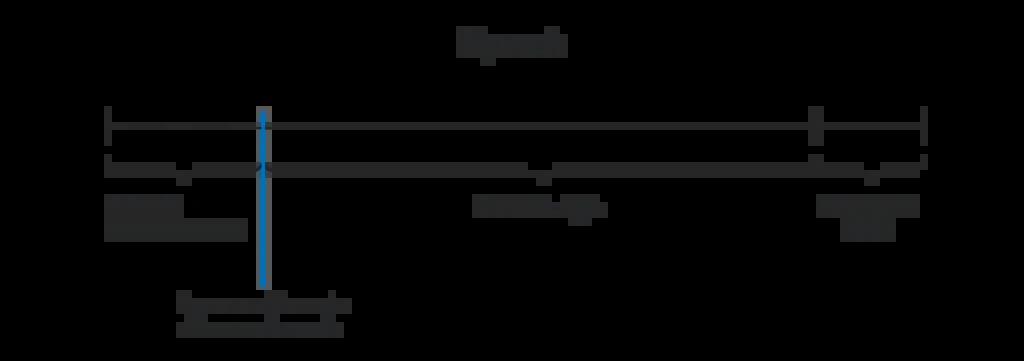
假如某個區塊生產者收到無效的公開份額，而且沒有及時在DKG過程中提出挑戰，則該礦工也無法在該時段中參與隨機數生成。請注意，只要其他k個誠實的參與者都能正確計算出份額，協議仍將正常運作。證明

還剩下最后一個問題：我們如何以不透露p(i)為前提，證明自己公布的H_i等于p(i)H？回想一下，每個參與者都知道H、G、p(i)G的值。在給定p(i)G和G的情況下回推p(i)的運算被稱為離散對數問題，又簡稱為dlog。那么每個參與者想做的都是：既能向他人證明dlog(p(i)G,G)=dlog(H_i,H)，又不會透露p(i)。的確存在這么一種方法構建上述證明，其中之一就是——Schnorr協議；通過Schnorr協議，參與者能在發布H_i時附上H_i的正確性證明。回想一下，隨機信標連的輸出是H_0的內插值。對于沒有參與生成隨機信標輸出的人來說，除了H_0，還需要哪些信息來驗證這個值的正確性？因為每個人都能自行在本地計算中加入G_0，所以只要證明dlog(G_0,G)=dlog(H_0,H)就行了。但因為信標的特性，我們無法得知p(0)，也就無法通過Schnorr協議生成這樣的證明。所以如果你要向其他人證明H_0的正確性，就必須保留所有H_i的值及其相應的證明。不過，好消息是，如果有些計算類似于橢圓曲線點乘法，則只需驗證H_0×G=G_0×H即可證明H_0的計算正確無誤。如果所選的橢圓曲線支持橢圓曲線配對運算，則這種證明是可行的。在這種情況下，任何知道G，H和G_0的人都可以核實H_0；而且H_0也可視作一個集體的多重簽名，證明區塊n的正確性得到至少k位參與者的檢查認證。目前我們還未在NEAR中使用橢圓曲線配對運算，但未來我們可能會使用，然后利用上文討論的小技巧取代我們當前使用的單一簽名方法。另一方面，DFinity使用BLS簽名，可以利用配對運算來實現上述簽名。

Tags：區塊鏈加密貨幣DLOLIBRA區塊鏈是什么概念哪些國家禁止加密貨幣DLO幣libra幣多少錢一個

TUSD