PLO:密碼專欄 | 超強進階：PLONK VS Groth16（下）

前言

本篇是“PLONKVSGroth16”的下篇，在上篇中我們對PLONK作了簡要介紹，分析了PLONK和Groth16算法在「可信驗證」和「約束構建」上的異同。那么，接下來讓我們一起看看在后續的「證明生成」和「驗證階段」兩者將有怎樣的差異，以及整體上的性能區別。

證明生成

對于程序qeval,prover需要證明自己知道qeval(x)=35的解，即x=3。

defqeval(x):

y=x**3

returnx+y+5

在上篇中我們已經介紹了PLONK的約束形式：門約束與線約束。繼續使用之前的例子，約束意味著零知識證明系統將這個問題約束成了一組格式固定的數學表達式，即問題描述等價于約束描述。而如果證明者真的知道這個問題的答案，將答案和計算中的中間參數代入約束表達式，這個組表達式必將是成立的。反之，如果該Prover提供的一組解無法使表達式成立，說明prover并不具備關于該問題解的知識。

黑客在多個Worldcoin Orb運營商的設備上安裝了竊取密碼的惡意軟件:金色財經報道，黑客在多個Worldcoin Orb運營商的設備上安裝了竊取密碼的惡意軟件，使他們能夠完全訪問Worldcoin運營商的儀表板。Worldcoin發言人Jannick Preiwisch表示，“一項內部調查得出結論，沒有敏感或個人用戶數據被訪問或泄露。Orb操作員永遠無法訪問任何敏感數據，并且任何生物識別數據捕獲在靜態和傳輸中都是加密的。”

Preiwisch補充說，“我們認真對待有關我們系統安全性和完整性的任何和所有索賠，并在收到對此類問題的詢問后立即進行調查，出于“高度謹慎”，該公司已重置Worldcoin運營商的所有登錄信息，并加快了Worldcoin運營商應用程序2FA的推出。”[2023/5/13 15:00:27]

這是最樸素的證明驗證思路，可以將它看作是“鎖”和“鑰匙的配對“：該問題約束的構建類似于“打造門鎖“，而針對該問題提供的一組解信息就是”一把開啟門鎖的鑰匙“。顯然，Prover可以舉著自己的解交給驗證者來驗證。可是這違背了我們的零知識原則：Verifier不應該獲取到Prover的隱私信息。

CZ：密碼管理器LastPass遭遇泄露，用戶需要確保已啟用2FA雙因子驗證:金色財經報道，據幣安首席執行官CZ在社交媒體透露密碼管理器LastPass遭遇泄露問題，CZ稱自己曾在博客文章中推薦過這個密碼管理器。據LastPass稱本次問題對客戶密碼沒有影響，因為客戶需要自己在客戶端加密，但黑客目前已經擁有了用戶信息，包括未加密的電子郵件地址和網站URL。盡管LastPass隨后提供了更新，但CZ仍提示如果重復使用主密碼的密碼或主密碼較弱，則黑客有可能獲得所有憑據，另外用戶需要確保已啟用2FA雙因子驗證。據此前報道，LastPass于今年八月部分源碼泄露。[2022/12/24 22:04:28]

那么有什么方法能在解鎖的同時保護隱私信息呢？

這里我們用到一個簡單的數學小技巧：減除，對此不太了解的讀者可查閱文章最后的前置知識。在前文《超強進階：PLONKVSGroth16》我們已經對從約束系統轉化到多項式進行了詳細的描述，在此我們不再贅述具體的轉化過程，但需要重復的一點是：根據生成時使用的點值對，生成的多項式在這些點處的取值將恒為0。PLONK同理，此處我們給出兩種算法的約束系統轉化為多項式后的形式。

動態 | 超3300萬個郵箱密碼泄漏，攻擊者勒索比特幣贖金:7月9日，騰訊御見威脅情報中心發文稱近期捕獲到一起挖礦木馬攻擊事件，該木馬病的獨特亮點就是利用肉雞電腦大量發送恐嚇勒索郵件。截止目前，該病已經攻克了1691臺服務器，已驗證的郵箱帳號超過3300萬個，包括Yahoo、Google、AOL、微軟在內的郵箱服務均在被攻擊之列，最終可能會有上億個郵箱帳號被驗證。如果郵箱帳號驗證成功就向該郵箱發送欺詐勒索郵件，郵件內容就是“我知道了你的密碼或隱私信息，你必須在X日內向XXX帳號支付價值XXX美元的比特幣，否則，就公開你的隱私信息。” 分析發現，病主模塊編寫者為“Burimi”，且具有內網傳播能力（感染U盤和網絡共享目錄），安全專家將其命名為“Burimi”挖礦蠕蟲。[2019/7/9]

Groth16:

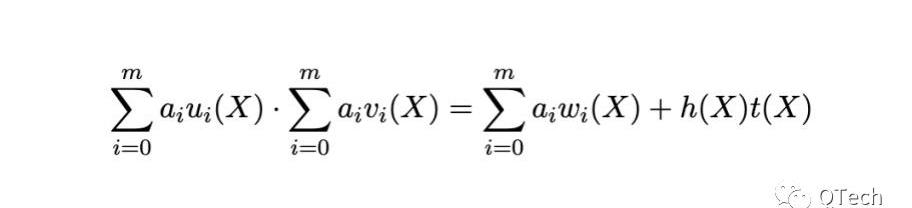
聲音 | 澳本聰：無法忍受阿桑奇那樣的人，比特幣從來就不是一個密碼朋克實驗:據ethereumworldnews消息，6月6日，澳本聰發文稱：“比特幣從來就不是一個密碼朋克實驗。我在90年代脫離了密碼朋克郵件列表，因為我無法忍受像朱利安·阿桑奇（Julian Assange）那樣的人。我無法忍受那里的一些人所代表的立場和觀點。我和密碼朋克郵件列表上的許多人正好相反。即使是那些我喜歡的人，比如Tim May，也持有一些我無法忍受的觀點。” 值得一提的是，盡管澳本聰不支持這些人，但密碼朋克在其宣言中呈現的哲學理念不僅與比特幣白皮書中解釋的理念非常相似，而且與中本聰在比特幣早期的思考方式也非常相似。[2019/6/9]

PLONK:?我們設門約束多項式為D(X)，線約束多項式為L(X)，那么PLONK的整個約束多項式將被表示為：

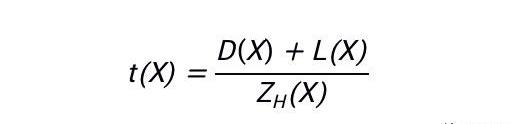
聲音 | Roger Ver：BCH是一種使用密碼技術的經濟系統:Roger Ver今日在其社交媒體表示看好BCH，稱贊其為一種使用密碼技術的經濟系統。[2018/9/11]

可以看到，兩者都使用了減除的思路，也就是這里的h(X)和ZH(X)，其具體內容取決于構建約束多項式時取的點值。

證明與驗證

同樣在之前的文章中，我們可以看到Groth16的證明規模極小，只包含三個群元素A,B,C。然而，這樣優雅的證明實現依賴于它的非通用可信設置，這也是Groth16的一大痛點。在Groth16中，證明方提供A，B，C，驗證方基于可信設置提供的參數，構建一個配對驗證等式。在驗證過程中包含了三次配對操作，也就是對驗證性能影響較大的耗時運算。Groth16的具體證明驗證如下所示。

Groth16證明：

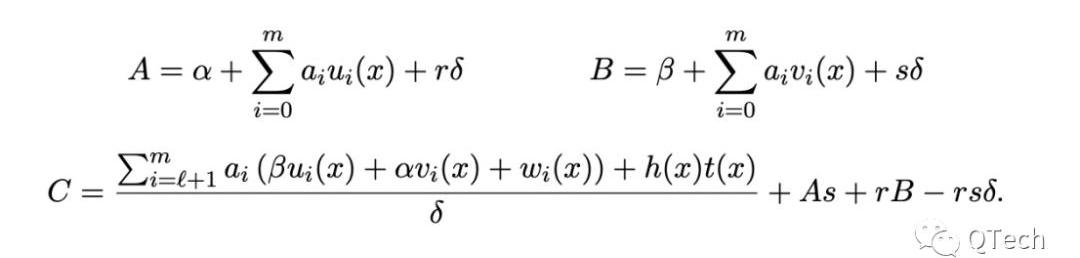
Groth16驗證：

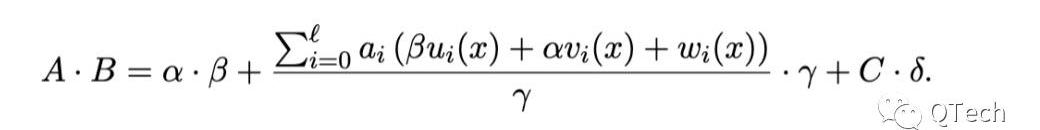
相比之下，PLONK的證明驗證將會復雜得多，這也是使用通用可信設置付出的代價。從驗證方角度看，由于可信設置參數缺少了包含問題具體內容，從而無法幫助其構建一些制約證明多項式的值。因此，如何固定住證明多項式的內容成為一個難題。PLONK使用的一個思路是引入Kate承諾。

結合前述的約束多項式，我們可以對t(x)中出現的每一項都構建一個承諾，以實現驗證方的驗證。PLONK證明的具體內容如下，包含了兩個點處的驗證：Wz(X)為多個多項式的同點承諾，Wzw(X)則為另一個點處的對z(X)的承諾。

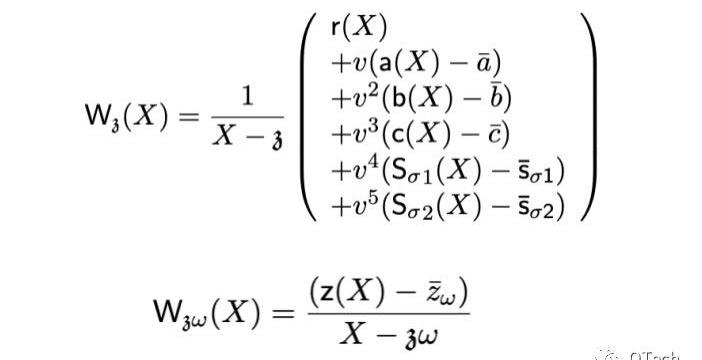
最后，PLONK的驗證在原文中也被歸納為一個簡潔的公式，實際上就是將上面提到的兩個點處的承諾簡單相加，具體等式如下所示：

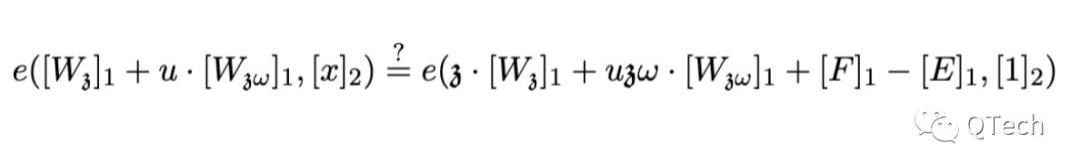
以上就是PLONK和Groth16算法內容的具體對比結果，講了這么多冗長的公式變換，兩者在性能層面的差距究竟如何呢？

性能比較

在這里我們給出的是PLONK論文中的結論。Table1是在證明階段的一個性能比較，Table2則是驗證階段的性能。可以看出，在驗證上，兩者的差距不大，Groth16比PLONK多了一次配對運算；而在證明方面我們遺憾地發現，Groth16不論在證明的工作量還是證明長度上仍然保持著最優的性能。但需要指出的是PLONK，尤其當它工作在fast模式時，所使用的SRS長度是所有算法中最短的。

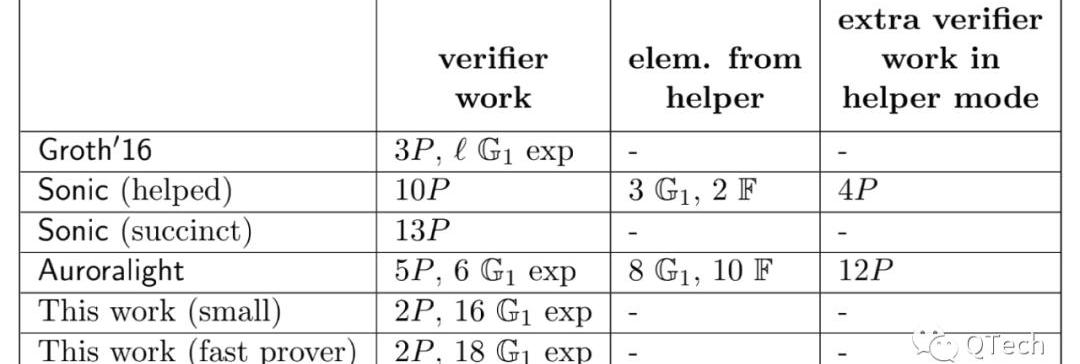
▲驗證階段性能比較

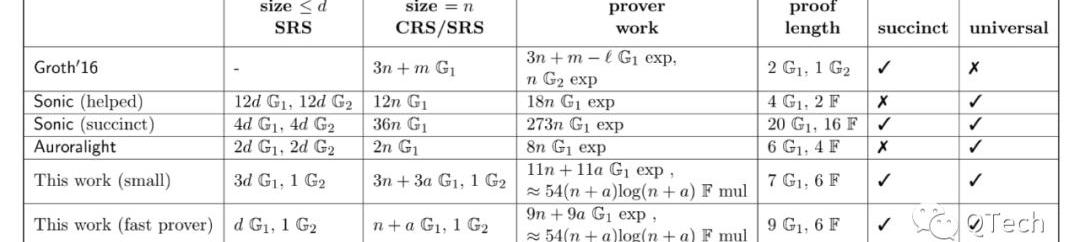
▲證明階段性能比較

前置知識

多項式減除

顧名思義，化減為除：若我們需要證明一個多項式f(x)在點a的取值為b，也就是證明f(a)-b=0；那么我們可以將其轉換為證明多項式f(x)-b可以整除(x-a)。其數學表示：

設多項式f(x)且f(a)=b，則存在一個多項式g(x)，使得：f(x)-b=g(x)(x-a)

kate承諾Kate承諾是由Kate，Zaverucha和Goldberg在2010年提出的一種多項式承諾方案。Kate承諾有多種形式，本文僅介紹PLONK中使用的常用形式，詳細可參考其paper中的相應內容。其常用形式可以概括為對多項式的隱藏和部分打開驗證。針對多項式f(x)，Kate承諾的具體步驟如下：

1）構造f(x)在點a處的承諾C

C：f(a)

2）選取點z，執行f(z)的opening

gz(x)=f(x)-f(z)/x-z

wz=gz(x)

3）給定f(z),C和Wz，驗證Kate承諾

C=wz*(a-z)+f(z)

以上就是“PLONKVSGroth16”的全部內容，如有任何疑問，歡迎添加小助手桔子加入技術交流群，在這里，你想知道的都會得到解答～

A.Kate,G.M.Zaverucha,andI.Goldberg.Constant-sizecommitmentstopolynomialsandtheirapplications.pages177–194,2010.

ArielGabizonandZacharyJ.WilliamsonandOanaCiobotaru.PLONK:PermutationsoverLagrange-basesforOecumenicalNoninteractiveargumentsofKnowledge.2019.

Tags：PLOLONGROROTPlotXPOKELONGROW價格Perpetual Protocol

Filecoin