DEFI:科普之密碼專欄 | 動手計算雙線性對（中）

前言

上一篇分享了“模運算”相關的知識，并且計算了一些有限域的例子，這一篇我們討論在通用零知識證明中經常提到的橢圓曲線和雙線性配對。橢圓曲線作為雙線性對的基礎和前置知識，我們首先介紹一下其在實數域上的表現形式，然后通過計算的方法列出”F_101”和其擴域“F_101^2”上的全部元素的列表。

橢圓曲線相關知識---曲線方程

橢圓曲線的一般形式的方程其實比較復雜，稱為Weierstrass方程，形如下面的形式：

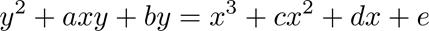
我們先將a,b,c,d,e隨意的取值為1,2,3,4,5，并通過畫圖來查看曲線在直角坐標系上的表現形式。根據二次方程求根公式，我們將其變換為x關于y的函數

歐易OKEx將于3月18日推出DeFi系列科普視頻:據歐易OKEx官方消息顯示，歐易OKEx將正式推出DeFi系列科普視頻《歐易DeFi20講》，本系列節目由歐易OKEx亞太區CEO馬克金主講。該視頻首期將于3月18日11:00(HKT)推出，用戶可以在歐易OKEx官方學院、金色財經觀看。

《歐易DeFi20講》主要包含DeFi入門指南、全景解讀DeFi生態及如何參與DeFi三個篇章，可以輕松使用戶了解DeFi原理，洞察DeFi價值，掌握DeFi熱點，更多詳情請關注歐易OKEx官方學院。[2021/3/18 18:55:59]

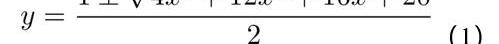
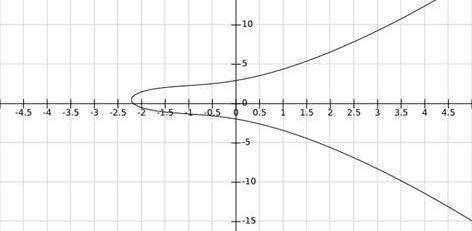
根據方程作圖如下：

TRON數字錢包科普資料《波場錢包的現在過去與未來》已上線:據最新消息顯示，由TokenPocket聯合波場TRON官方，以及 TokenPocket 社區志愿者共同撰寫的《波場錢包的現在過去與未來》已正式上線。《波場錢包的現在過去與未來》又稱為波場錢包小白書，詳細介紹了當前TRON錢包與TRON生態密切結合的實例，是目前市面上最為詳細的TRON數字錢包科普資料。波場錢包作為波場公鏈生態中極為重要的入口，是波場生態的重要構成要素。波場錢包從一開始只提供權限管理、轉賬收款、節點投票等基礎功能，到如今不僅可以為用戶提供法幣交易、閃兌和去中心化交易所等方便快捷的交易服務，還能讓用戶直接在錢包上體驗波場上DApp，挖礦、DeFi、Staking等資產增值服務。詳情見原文鏈接。[2020/8/20]

根據上面的方程和作圖過程了解道，曲線由上下兩個半支組成，關于y=0.5對稱。

對稱的總是美的，但是這個曲線卻有一點瑕疵，他的對稱軸并不是x軸而是y=0.5。考慮到Weierstrass太過復雜，人們更經常使用的是在Weierstrass方程的基礎上進行一些坐標變換和參數化簡后的形式。新的形式關于x軸對稱。

動態 | 報告：區塊鏈等熱點詞促使童書科普百科類成交額同比增速最高:近日，京東圖書與艾瑞咨詢聯合發布了《2019中國圖書市場報告》。報告指出，AI、5G、區塊鏈、機器人、VR、智能家居、AR這些熱點詞，不斷點燃科技熱潮，科技在改變大眾生活的同時，也吸引了越來越多家長的關注，從小培養孩子對科技的興趣和熱愛。因此童書中科普百科類成交額同比增速最高，占比將近40%。[2020/1/8]

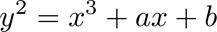
當取a=0，b=3時，畫出曲線如下圖，容易驗證是曲線上一點，對稱的也是。

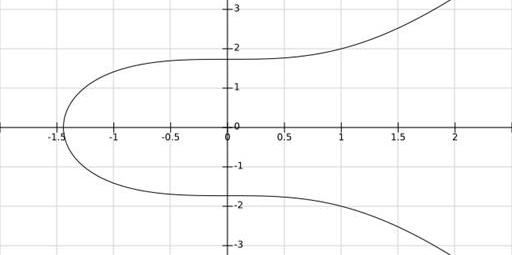
通過方程我們畫出了曲線y^2=x^3+3的圖像，但是說這就是橢圓曲線的圖像其實并不準確。準確地說，我們畫的是在實數域上這個方程的圖像。在復數域上當然有更多的點也滿足曲線方程但是我們的圖像中并沒有體現，例如。如果把曲線看作點的集合，那數域的擴張直接影響到我們要討論的這個集合的大小，這在本文后半部分我們還會看到。

動態 | 幣安科普MimbleWimble算法:幣安官方推特今日發布隱私算法Mimblewimble的科普貼，在下方留言區大量網友留言猜測是否是基于 Mimblewimble算法的隱私幣Grin或者Beam即將登陸幣安交易所，其中猜測Grin的呼聲更高。[2019/9/2]

另外為了讓其擁有更多的性質，我們認為橢圓曲線其實還包括一個“無窮遠”點。這個點在圖中并不能體現出來，我們也不能以直角坐標的形式寫出這個點的坐標，但是當我們說橢圓曲線時默認其點的集合中包含這個點。“無窮遠點”一般用"O?"表示。

橢圓曲線相關知識---點的運算

就像討論“F_7”時那樣，有了元素的集合還需要有在集合上的運算。這條曲線就是橢圓曲線點的集合，但是為了構建密碼算法還需要定義點的運算。不同于域中需要兩種基本運算，這里我們只需要定義一種特殊的基本運算就可以，不妨將這種運算稱作加法，用“+”表示。

通過幾何意義可以清楚的理解這種運算的定義，例如我們選取了曲線上的兩個點A和B計算加法，把A+B的結果記為C，過程如下：

動態 | 浙江衛視節目科普支付寶區塊鏈防偽溯源產品:昨日，在浙江衛視播出的科普綜藝欄目《智造將來》現場，支付寶首次展示了支付寶區塊鏈防偽溯源產品，以接地氣的方式公開向大眾展示區塊鏈在生活中的應用。[2019/3/4]

1）過AB做直線，交曲線于T；

2）過T做x軸垂線，交曲線于C點，C即為所求；

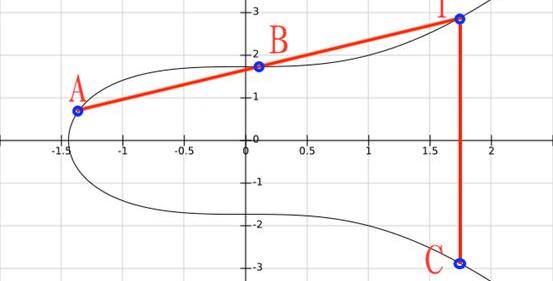
需要說明的是，當兩個“加數”位置的點為同一個點時，步驟一中所做的其實是過該點的切線。另外，當AB的連線本身就垂直于x軸時，我們規定AB和曲線的第三個交點是無窮遠點“O”。

在這樣的規則下容易發現，任何點P都有一個對應的P’,使得P+P’=O；并且任何點A和O的運算的結果都是A本身。而且因為連線AB和連線BA其實是同一條直線，因此我們也能夠得知這里定義的點的加法是滿足交換率的。

根據定義再結合一些解析幾何的知識，就可以求出點加法的坐標計算公式。例如假設A和B的坐標分別為(Xa,Yb)和(Xa,Yb),那么C點坐標如下：

其中"λ"是直線AB連線的斜率，或者當A、B重合時是A點的切線斜率。

現在我們將轉而討論有限域上的橢圓曲線，其上的橢圓曲線表現為一些散布的點。在有限域上A+B雖然已經沒有明確的幾何意義，但是有同樣的計算公式。我們已經驗證過是橢圓曲線上的點，那么我們就把該點記為G，并且從該點開始，計算G,G+G，G+G+G...看看會有怎樣的規律。

以G+G為例，我們進行演算,首先計算λ，也就是G點的斜率：

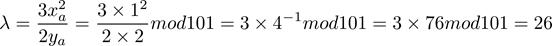
然后計算C點坐標：

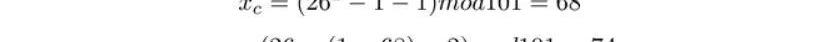
因此G+G的坐標為。而G+2G稍稍有不同，主要是λ需要從切線斜率修改為過AB的直線斜率：

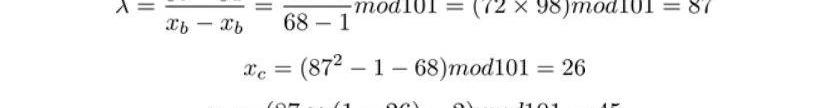
因此我們也計算出G+2G=3G的坐標，以此類推進行計算，我們得到下表

讀者可以選擇表中的點，例如(32,42)，來驗證其是否在曲線上，也就是是否滿足曲線方程y^2=x^3+3mod101，相關演算我們不在本文贅述。

經過計算和驗證可以發現，這一系列點構成了一個周期為17的循環。如果我們將k個G相加記為kG，并且將O看作0G，那么有17G=O。這像極了模17加法的規律，并且在模17加法和為0的兩個數對應的兩個橢圓曲線點的和正好是O，我們說這樣的17個點和加法一起構成一個有17個元素的循環群。因為這只是一篇科普性質的文章，我們不給出循環群的嚴格定義，但是正如它的名字中強調的“循環”，循環群最突出的性質就是能夠由某個元素不斷運算從而得到全部。

需要強調的是這17個點并不是F_101上橢圓曲線的全部，但僅利用這17個元素組成的集合我們已經能夠在其中完成點的加法運算，也就是說任意選擇集合中兩個點進行加法，其結果不會跳出到集合之外。

在本篇最后，我們展示17個點在直角坐標系中的分布，讀者可以體會其中的對稱之美。下一篇我們將找到另一個17個元素的循環群并且在其基礎上計算雙線性映射，敬請期待。

附錄

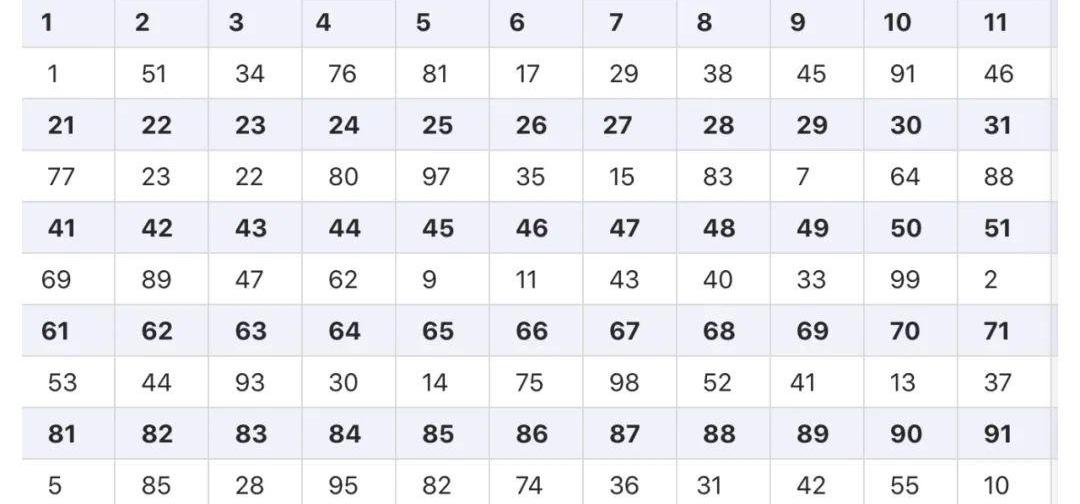
▲表2：模101元素逆元表

喬沛楊

趣鏈科技基礎平臺區塊鏈底層密碼學小組

Tags：DEFIEFIDEFokexTRD-DeFiDeFi.ch99DEFI.NETWORKokex官方網頁版

MANA