萬字長文，詳述TRIDENT: Poseidon 哈希算法的硬件加速與實現！

本文主要介紹了DatenLord團隊在今年的Xilinx全球自適應計算挑戰賽上獲得BigDataAnalytics賽道一等獎的作品——TRIDENT:Poseidon哈希算法的硬件實現與加速。該項目基于XilinxVariumC1100FPGA加速卡，為Filecoin區塊鏈應用中的Poseidon哈希算法提供了一套完整的硬件加速方案。在硬件方面，TRIDENT基于SpinalHDL設計了Poseidon加速器IP并基于Vivado中BlockDesign工具搭建完整的FPGA硬件系統。在軟件方面，我們為Filecoin軟件實現Lotus提供了訪問FPGA硬件加速器的接口。最終，TRIDENT能夠為Filecoin應用提供兩倍于AMDRyzen5900X處理器的Poseidon計算加速效果。下文將主要從Poseidon哈希算法概述、基于SpinalHDL和Cocotb的硬件設計、總體方案設計、加速器IP設計和性能測試等方面對整個TRIDENT項目進行詳細的介紹。

引言

Poseidon是一種全新的面向零知識證明(ZKP:Zero-KnowledgeProof)密碼學協議設計的哈希算法。相比同類算法，包括經典的SHA-256、SHA-3以及Pedersen哈希函數，在零知識證明的應用場景下，Poseidon能夠顯著地降低證明生成和驗證的計算復雜度，極大地提升零知識證明系統整體的運行效率。基于上述優點，Poseidon目前已被廣泛應用在了各種區塊鏈項目當中，包括去中心化存儲系統Filecoin、加密貨幣MinaProtocol和DuskNetwork等，主要用于加速其中的零知識證明系統。

0.1Poseidon與零知識證明

零知識證明(ZKP:Zero-KnowledgeProof)是一類用于驗證計算完整性(ComputationalIntegrity)的密碼學協議。其基本的思想是:使證明者(Prover)能夠在不泄露任何有效信息的情況下向驗證者(Verifier)證明某個計算等式(ComputationalStatement)的成立。一個具體的證明對象可以表示為如下形式：

f=(x,w)

其中f代表某個函數或程序,x代表該函數中公開的輸入,w表示需要保密的函數輸入，即只有證明者知曉。在零知識證明系統下,證明者能夠在不泄露w的情況下向驗證者證明該等式的成立。由以上描述可見，零知識證明最顯著的特點也是其最大的優勢在于隱私保護性，證明者可以在不泄露任何重要私密信息的情況下完成對某個函數或程序的計算結果的證明。

由于零知識證明能夠兼顧計算完整性證明和隱私保護,其具備廣泛的應用場景,具體包括匿名線上拍賣、匿名電子投票、云數據庫SQL查詢驗證、去中心化數據存儲系統等。尤其是在區塊鏈和加密貨幣領域，零知識證明憑借其出色的隱私保護特性,近年來獲得了大量開發者和設計者的青睞,包括加密貨幣Zcash和Pinocchio以及分布式存儲系統Filecoin等在其設計中都采用了ZK-SNARK零知識證明算法。

為了保證證明算法的通用性，零知識證明通常不會針對某一特定的函數f而設計。如果需要驗證上述公式的成立，需要將具體的f函數轉換到零知識證明算法所規定的受限表達式系統(ConstraintSystem)當中，這一過程可以理解為“程序編譯”,即將待證明的程序轉換成另一種由受限表達式(Constraints)組合成的具備相同功能的程序。例如對于ZK-SNARKs算法，需要將待證函數轉換成由特殊的二次多項式R1CS(R1CS:Rank-1QuadraticConstraints)組成的程序。而轉換后的函數形式也被稱為算數電路(ArithmeticCircuit),證明者和驗證者都需要在該電路的基礎上進行一系列的算術運算來完成證明生成和驗證的工作。

雖然零知識證明能在提供計算完整性驗證的同時兼顧隱私的保護,但其代價是提高了證明生成和驗證的計算復雜度。目前，不論對于證明者還是驗證者完成一次零知識證明都需要消耗大量計算資源。通常情況下,證明生成和驗證的計算復雜度和待證函數f轉換到受限表達式系統后的復雜度,即轉換結果所包含的受限表達式的數量成正比關系。不同待證函數經過“編譯”后生成的受限表達式的數量不同,所需計算的復雜度以及對應的證明生成和驗證的時間也有很大的差異。在區塊鏈應用中，待驗證的函數通常與某種哈希函數相關。而TRIDENT所加速的Poseidon哈希算法對零知識證明做了針對性的優化，使得其對受限表達式系統的適配程度顯著優于同類的算法。例如，Poseidon哈希算法轉換后所需的受限表達式的數量是同類Pedersen哈希函數的八分之一左右,這意味著Poseidon完成零知識證明所需的計算量將顯著地降低，同時整個零知識證明系統的效率也會得到大幅提升。

0.2Filecoin分布式存儲網絡

TRIDENT項目中實現的Poseidon加速器主要針對的是應用在Filecoin分布式存儲網絡中的Poseidon哈希計算實例。Filecoin在提供存儲服務過程中需要對數據進行Poseidon哈希運算，這一計算過程需要消耗大量的算力，是整個Filecoin系統運行的性能瓶頸之一。

Filecoin是基于區塊鏈技術建立的一種去中心化、分布式、開源的云存儲網絡。其主網絡已平穩運行一年，并展現出了高速、低成本和穩定的特點。由于其開源、去中心化的優點，目前Filecoin已經得到了廣泛的應用，包括著名的維基百科(Wikipedia)已將其網站的數據庫存儲在Filecoin網絡上。在Filecoin中主要有兩種角色，分別是用戶(Client)和礦工(Miner)，其基本的運行機制是：Client發出數據存儲或檢索的需求并支付文件幣，而礦工通過提供存儲服務檢索服務獲得相應的獎勵。

FTX客戶索賠門戶網站啟動時間推遲:7月3日消息，FTX官方對此前公布的FTX客戶索賠門戶網站的啟動時間作出了更改，此前為將于2023年7月3日左右簽署與該動議相關的法院命令后啟動，已改成由于最近對提交的時間表進行了修改，該門戶網站將在未來幾周內啟動。

不過網站提示稱，當門戶網站開放時，客戶將通過電子郵件和FTX官方推特帳戶收到通知。[2023/7/3 22:15:06]

與傳統的由數據中心提供的云存儲服務不同,任何具備空閑存儲資源的設備均可以在Filecoin網絡上提供存儲服務。因此，為了保證存儲服務的質量，Filecoin中分別設計了包括復制證明PoRep(ProofOfReplication)和時空證明PoSt(ProofOfSpacetime)等機制來保證數據存儲的完整性和持久性，而這些機制中涉及大量的密碼學算法，包括哈希算法SHA-256和Poseidon以及零知識證明zk-SNARK等，需要大量的算力支持。目前這些算法主要是基于GPU實現計算加速，并沒有相關開源的FPGA硬件加速方案。

目前，應用最為廣泛的Filecoin軟件實現是由ProtocolLabs基于Go語言編寫的Lotus。可以將Lotus理解為用戶與整個Filecoin存儲網絡進行交互的接口。具體來講，Lotus是一個在Linux操作系統上運行的命令行應用程序，其所提供的功能包括:1)上傳和下載文件；2)將空閑的存儲空間出租給其他用戶；3)檢查計算機存儲數據的完整性等。同時，Lotus中提供了用于測試計算機硬件在Filecoin計算負載下性能表現的基準程序Lotus-Bench。

TRIDENT項目在Poseidon加速電路的基礎上，為Lotus提供了訪問底層FPGA硬件加速器的軟件接口，進而通過Lotus-Bench對加速器的計算性能進行了測試和比較。

Poseidon哈希算法概述

1.1Poseidon參數

準確地說，Poseidon指的是一類具有相似計算流程的針對零知識證明算法而優化的哈希函數的集合。類比編程語言中面向對象的概念,可以將Poseidon理解成一個哈希函數類,該類需要若干基本的初始化參數。在應用過程中,需要通過初始化這些基本參數生成具體的哈希計算實例。而不同參數組合對應的Poseidon實例,雖然在計算流程上基本相似,但在安全性、計算量和復雜度等方面都有一定程度上的差異。Poseidon哈希函數類初始化的所需的基本參數為(p,M,t),由這三個參數可確定一個唯一的哈希計算實例。

在這三個基本參數的基礎上，可計算出其他與Poseidon計算流程相關的參數，包括：

對于TRIDENT所要加速的FilecoinPoseidon計算實例，各個參數的取值如下：

其中參數的16進制表達式為：

p=0x73eda753299d7d483339d80809a1d80553bda402fffe5bfeffffffff00000001

參數p的實際位寬為255位，哈希函數中的所有算術運算操作均在p確定的有限域內完成，即所有的算術運算均是模數為p的模運算，包括255-bit模加和255-bit模乘；同時，參數p還確定了S-Box階段模冪運算的指數α=5；

FilecoinPoseidon實例的參數t∈{3,5,9,12}，即Poseidon實例計算的中間狀態可以包含3、5、9或12個有限域元素；

FilecoinPoseidon實例的安全等級M=128Bits，安全等級M和參數P共同確定了FullRound迭代次數RF=8以及PartialRound迭代次數RP∈{55,56,57,57}(依次對應的四個取值)；

1.2Poseidon詳細計算流程

從輸入和輸出的角度看，Poseidon哈希函數將輸入的(t?1)個有限域元素映射到一個輸出有限域元素。對于本次課題加速的FilecoinPoseidon實例，參數t∈{3,5,9,12}，因此其輸入數據所包含的元素個數可以是2，4，8或12，輸出為一個元素，由于參數P的位寬為255位，所以輸入輸出有限域元素的位寬也同樣為255位。

Poseidon的詳細計算步驟可表述如下：

1.初始化：將輸入preimage的(t?1)個元素通過拼接(Concatenation)和填充(Padding)的方式轉換成包含t個有限域元素的中間狀態state;

2.進行RF/2次FullRound循環：每次循環中需要對state向量的所有元素依次完成AddRoundConstant，S-Box和MDSMixing操作，其中AddRoundConstants需要完成一次常數加法，S-Box需要計算五次模冪，MDSMixng計算的是state向量和常數矩陣M相乘;

3.進行RP次PartialRound循環：PartialRound循環和FullRound循環的計算流程基本一致，不同點在于PartialRound在S-Box階段只需完成第一個元素的模冪運算；

BRC-20代幣總市值突破7億美元:金色財經報道，數據顯示，比特幣銘文代幣Ordi突破19美元，暫報19.58美元，24小時漲幅17.96%，當前總市值已達4.11億美元。此外，BRC-20相關代幣目前約為14200種，總市值突破7億美元，過去24小時的交易量為203996187美元。

據悉，BRC-20協議是直接寫到比特幣網絡上，以聰為載體，用OrdinalInscriptions的JSON數據部署、鑄造和轉移代幣。Ordi是第一個比特幣銘文代幣，總供應量為2100萬枚。[2023/5/9 14:51:11]

4.進行RF/2次FullRound循環：計算流程與步驟2一致；

5.輸出：在完成步驟1-4中總共(RF+RP)次循環后，將state向量中的第二個元素作為哈希運算的結果輸出；

即上述算法2-8步驟對應的計算流程圖如下：

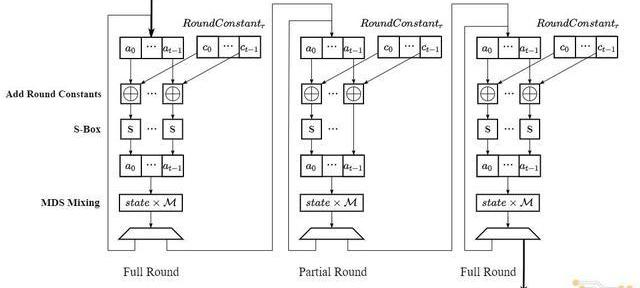
1.3Poseidon算法特點

上文提到，Poseidon可以看成是一類相似的哈希函數實例組成的集合，這類哈希函數計算流程的共同特點包括：

所有運算均在有限域內完成，即均為模運算；計算過程中涉及大量的常數，包括和常數相加以及和常數矩陣相乘；整體計算流程由多次相同的迭代組成，這些迭代可以分成fullround和partialround兩類；計算過程中涉及兩種高位寬的算數運算，分別是模加和模乘。以FilecoinPoseidon為例，其算數運算的操作數為255位；

上述四點簡要概括了整個Poseidon哈希計算的特點，也是硬件加速器設計與實現中需要著重考慮的幾個地方。本章第二節將結合詳細的計算流程進一步深入地介紹Poseidon哈希函數。

基于SpinalHDL和Cocotb的硬件設計與驗證

TRIDENT項目采用了基于Scala的硬件生成器語言SpinaHDL和基于Python的驗證框架Cocotb完成整個Poseidon加速器IP的設計與驗證。這兩種新興的硬件設計和驗證工具極大提升了整個加速器的開發效率和質量.

2.1SpinalHDL和Cocotb概述

和RISC-V處理器開發中常用的Chisel類似，SpinalHDL是一種基于高級編程語言Scala的硬件生成器語言HCL(HCL:HardwareConstructionLanguage)，更確切地說，它是一個用于數字硬件設計的Scala編程包。

對于開發者來說，SpinalHDL通常可以分成兩部分:Scala語法和SpinalHDL提供的電路元件抽象。SpinalHDL通過Scala語法中類和函數的形式提供了硬件設計所需的各種基本電路元件的抽象，包括寄存器、邏輯門、多路選擇器、譯碼器和算術運算電路等。而電路設計者所要完成的工作是：基于Scala的語法來描述電路的整體結構，即描述各個基本電路元件之間的連接關系。由于Scala是一門多范式的編程語言，其支持函數式編程、面向對象、遞歸等高級的語言特性，能夠賦予設計者強大的結構建模能力和代碼參數化的能力。

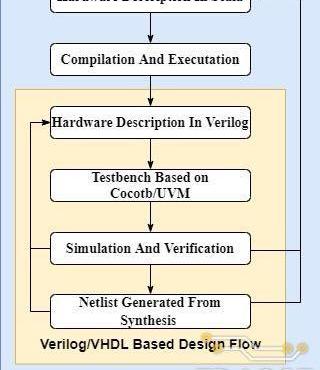
基于SpinalHDL的具體硬件開發流程如下：

使用Scala語法和SpinalHDL中提供的電路元件抽象描述所需的硬件電路結構;編譯并執行Scala代碼以生成對應的Verilog或VHDL代碼;使用SystemVerilog或Python語言搭建待測電路的驗證平臺；基于SynopsysVCS、VivadoSimulator或ModelSim等仿真器進行電路的功能仿真和驗證，若功能仿真的結果和預期不符，則返回步驟1繼續修改電路設計代碼；

使用DesignCompiler或VivadoSynthesis對通過功能驗證的RTL代碼進行綜合，生成對應的網表文件以及電路的時序、面積和功耗等信息。若綜合結果不滿足設計需求，則返回步驟1進一步優化電路結構。

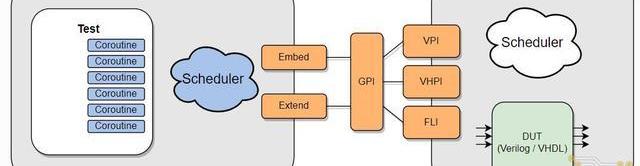
Cocotb是一種開源的基于Python的數字電路驗證框架，該驗證框架的具體工作模式如下圖所示。基于Cocotb的電路驗證可以分為如下兩個部分:

1.基于Python編寫的測試平臺代碼：基于Python中的協程(Coroutine)并行地完成：產生待測電路輸入端的激勵信號；將相同的激勵信號傳遞給參考模型得到標準輸出；監測待測電路的輸出端口，并檢查輸出結果是否和標準輸出一致；

2.支持標準GPI編程接口的電路仿真器：通過GPI編程接口接收Python測試代碼生成的輸入端激勵信號，并對待測電路DUT(DUT:DesignUnderTest)進行功能仿真

使用Cocotb進行電路功能仿真并不需要編寫額外的Verilog或VHDL代碼，測試中的所有工作，包括產生輸入激勵信號、參考模型的實現以及監測輸出結果等都可以在Python代碼中完成，而Python代碼可以通過仿真器提供的GPI編程接口與待測電路進行交互。借助Python高效簡潔的語法和強大的生態，驗證人員可以更加快速地實現驗證代碼的邏輯功能，加快硬件設計的迭代速度。

比特幣礦企Core Scientific向CEO附屬的私人飛機公司支付了超過100萬美元:金色財經報道，上周提交的破產法庭文件顯示，破產的比特幣礦企 Core Scientific (CORZ) 去年向 CEO Mike Levitt 的一家附屬公司支付了 165 萬美元，該公司經營一架私人飛機。私人飛機主要用于在偏遠地區的數據中心站點之間運送員工、客戶和潛在客戶。[2023/2/17 12:13:45]

2.2SpinalHDL在硬件設計中的優勢

本章的第一節提到，SpinalHDL對于開發者來說可以分成Scala語法和SpinalHDL提供的電路元件抽象兩部分，而其在電路設計上的優勢也主要源于這兩方面。從Scala的角度來說，其高級的語言特性，包括函數式編程、面向對象和遞歸等，能為設計者提供強大的電路建模能力。而從SpinalHDL自身的角度來說，其提供的豐富電路抽象使開發者避免了一些常用電路模塊的重復實現，從而能從更高的抽象層次進行電路的描述。下文將詳細描述SpinalHDL在電路設計中的四點優勢:

1.和Verilog相同的電路描述粒度：

數字電路建模的方式通常可以分成行為級和結構級兩種，如Verilog和VHDL就是從結構級對電路進行描述，而像高層次綜合HLS(HLS:HighLevelSynthesis)則是先通過高級編程語言描述算法行為，然后將其轉換成對應電路的RTL代碼。大多數情況下行為級建模能夠更加高效地完成電路設計，但往往通過這種方式得到的電路在性能和資源消耗上很難達到設計者的要求。

和高層次綜合HLS不同，SpinalHDL雖然也是基于高級編程語言Scala進行設計，但其本質上仍然是從結構級對電路進行描述。對于開發者來說，如果不使用Scala中的高級語言特性以及SpinalHDL中抽象層次較高的電路模型，諸如FIFO、計數器和總線仲裁器等，完全可以像使用Verilog一樣對電路進行建模。

2.更可靠的電路描述方式：

使用SpinalHDL進行電路描述能夠提升設計的可靠性，顯著地降低代碼出錯的概率。而代碼可靠性的提升不僅能減輕電路驗證的壓力，同時對后期的代碼維護也有很大的幫助。

3.更強的建模和表達能力:

SpinalHDL對電路強大的建模和表達能力主要源于Scala所提供的各種豐富的高級語言特性，包括函數式編程、面向對象以及遞歸等。此外，SpinalHDL自身提供的豐富的電路抽象使開發者能夠避免很多底層模塊的重復實現，進而從更高的層次構建電路。SpinalHDL中不僅提供了基本的電路元件如信號、邏輯運算符、算數運算符和寄存器等，同時也實現了諸如FIFO、AXI總線、計數器和狀態機等較高層級的電路模型。

4.更好的代碼復用能力：

除了更加強大的電路建模能力外，SpinalHDL還能為硬件設計代碼帶來更改好的復用性。硬件設計所要處理的問題經常都是高度定制化的，而Verilog中的“parameter”和“localparam”關鍵字往往不能提供足夠的參數化能力，一份代碼很難適用于不同的應用場景。而基于SpinalHDL和Scala，開發者可以通過復雜函數的實現和面向對象的語法特性，對電路模型進行更高層次地抽象和參數化設計，從而提升代碼的復用能力。

2.3Cocotb在驗證中的優勢

1.Python的語法特點：

相比傳統硬件驗證使用的語言，如Verilog、VHDL和SystemVerilog，Python具備更加高效和簡潔的表達能力。即使和C/C++以及Java這些軟件開發中的高級語言相比，Python在代碼開發效率上也有很大的優勢。此外，作為一門高級編程語言，Python同樣支持諸如面向對象等高級的語言特性，能提供很好的抽象和參數化的能力，幫助驗證人員構建復用性更高的驗證代碼。

以本次課題中Poseidon加速的驗證為例，Poseidon哈希算法需要完成大位寬數據(255位)的算術運算。而包括C/C++以及Java等大部分編程語言一般最高只支持64位整數運算，而Python中的整數類型支持任意位寬的數據，這一點大大降低了Poseidon加速器軟件參考模型實現的復雜度。

2.Python豐富的軟件生態：

同時Python擁有強大的生態和豐富的開源代碼庫。使用Cocotb進行硬件設計的驗證，可以很方便地復用這些現有的基于Python的算法實現，作為硬件電路的參考模型。例如，在設計深度學習相關的加速器時，可以基于Pytorch、Tensorflow和Caffe等Python庫搭建驗證用的深度學習算法的參考模型；對于SoC設計中涉及的各種總線協議，如AXI協議等，Cocotb中也提供了相應的開源軟件實現；而對于網絡協議相關的硬件實現，可以借助Python的網絡包數據處理工具Scapy庫搭建參考模型。使用Python現有的開源軟件包不僅能夠極大地減輕搭建參考模型的工作量，同也可降低代碼出錯的概率。

總體方案設計

3.1開發平臺

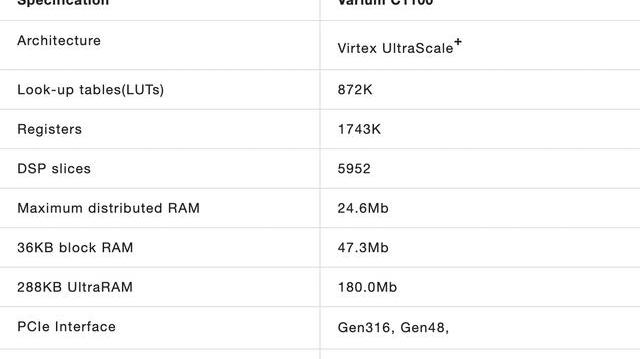
本次課題研究中使用的硬件開發平臺為Xilinx公司最新推出的面向區塊鏈應用的VariumC1100FPGA加速卡。整張加速卡的核心是基于XilinxVirtexUltraScale+架構的FPGA芯片，具體型號為XCU55N-FSVH2892-2L-E。該FPGA芯片配備了豐富的可編程硬件邏輯資源和高速的通訊接口，能夠支持區塊鏈應用中各種計算和訪存密集型算法的硬件實現。整個FPGA加速板卡的外形如下圖所示：

FTX債務人、巴哈馬清算人反對美國受托人提出的任命審查員請求:1月26日消息，監督FTX案件的美國受托人要求特拉華州破產法院允許任命第三方審查員調查FTX及其子公司的財務狀況。John Dorsey法官將在2月6日的聽證會上考慮該動議。 FTX債務人和巴哈馬聯合臨時清算人的律師提交了法庭文件，反對任命審查員。律師稱任命一名審查員調查FTX倒閉事件可能耗資近1億美元，并且對債權人沒有任何好處。（ The Block）[2023/1/26 11:30:49]

VariumC1100板卡各項詳細參數如下表所示。TRIDENT中主要使用到的硬件資源包括：1)LUT和寄存器資源:用于實現加速器電路的基本框架；2)DSPslices:算數運算單元的實現；3)RAM資源：用于存儲Poseidon計算中涉及的常數；4)寄存器；4)PCIe接口:實現加速器與服務器主機之間的高速通訊。此外，在開發方式上，C1100板卡既支持基于C/C++語言的VitisHLS高層次綜合工具，也可以在Vivado集成開發環境下使用RTL語言進行硬件設計。

3.2加速系統設計

TRIDENT中設計的FPGA加速系統的整體架構下圖所示。整個加速系統主要分為CPU服務器和FPGA加速卡兩個主體。CPU服務器運行Filecoin具體軟件實現Lotus提供數據存儲服務，當需要進行Poseidon哈希函數的計算時，服務器以DMA的方式將數據傳輸到Poseidon硬件加速器當中進行哈希計算。Poseidon加速器完成計算后以相同的方式將哈希結果傳回處理器內存中。

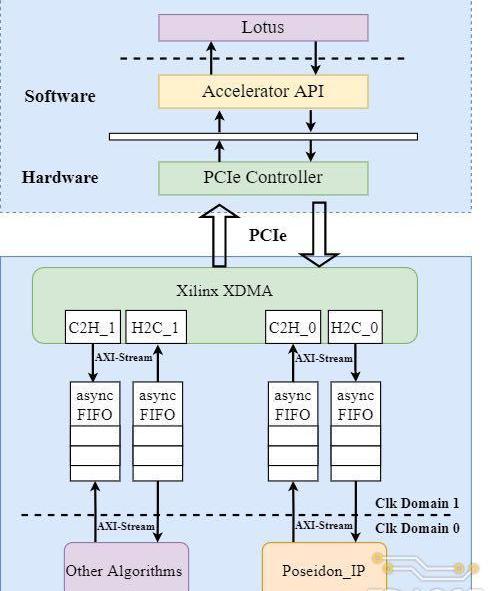
其中FPGA硬件系統主要由三個部分組成：

1.XilinxXDMAIP：實現數據從CPU側內存到FPGA的搬運；同時負責PCIe外設總線到FPGA片內AXI-Stream總線的轉換；

2.異步FIFO：實現XDMAIP到Poseidon加速器間跨時鐘域的數據傳輸；XDMA輸出的總線時鐘固定為250MHz，而Poseidon加速器IP的工作頻率在100-200MHz，且驅動兩部分硬件的時鐘源不同；

3.Poseidon加速器：整個FPGA加速卡的核心部分，負責Poseidon哈希函數的計算加速;目前，系統中只實現了Poseidon哈希函數的加速器，還可以通過增加XDMA通道數以接入其他哈希算法的硬件加速單元；

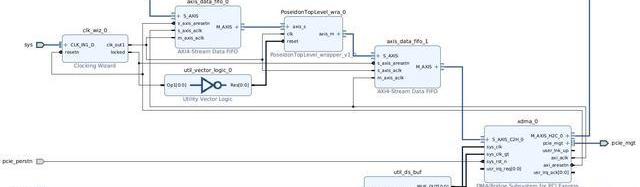
在上述系統架構設計的基礎上，本次課題研究中實際搭建的FPGA硬件系統如下。和上圖展示的硬件架構圖相比，實際的FPGA硬件系統中增加了UtilityBuffer、UtilityVectorLogic和ClockWizard等模塊來處理時鐘和復位信號。

加速器IP設計

在上述FPGA硬件系統整體架構設計的基礎上，本文的第四部分將介紹其中的核心模塊Poseidon加速器IP的設計與實現細節。對于任意算法的硬件加速器，其設計與實現大體上都可以分成單元運算電路和整體硬件架構兩部分。對于單元運算電路而言，諸如加法器、乘法器和模乘器等，其設計的主要目標是如何在更少的硬件開銷下達到更佳的計算性能。在單元運算電路的基礎上，硬件架構設計需要考慮的是如何提升每個運算單元的利用率，進而使加速器整體達到更高的數據吞吐率。本節將對Poseidon涉及的兩種模運算，包括模加和模乘的具體電路實現以及加速器硬件架構的設計做詳細地介紹。

4.1模加電路的設計

模運算是密碼學中核心的數學概念，大部分密碼學算法都是建立在模加和模乘的基礎之上。相比普通算術運算，模運算最大的特點就是所有的操作數和運算結果都在有限域(FiniteField)內，即不超過模運算所指定的模數。不論是模加還是模乘，基本上所有模運算的實現都可以分成普通算術運算和取余兩個步驟。對于模加，首先需要對兩個操作數完成一次普通加法運算，然后再將加法結果縮減到模數所規定的范圍內，具體的數學定義如下：

a⊕b=(a+b)modp

由于a和b都小于模數p，因此模加實現過程中取余的步驟通過減去模值p即可實現，具體的算法流程如下。

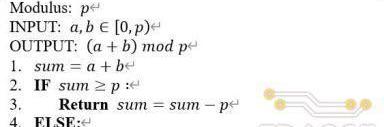
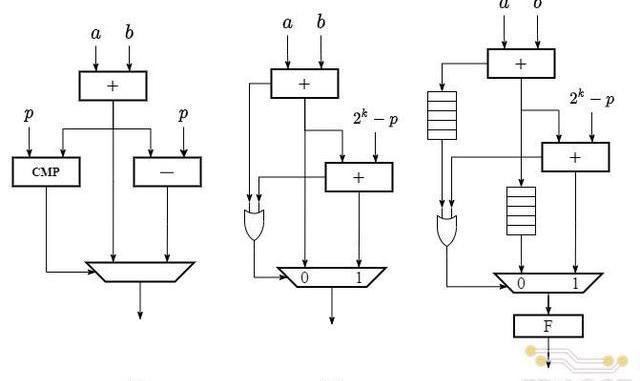
該算法對應硬件電路結構如下圖(a)所示,具體數據通路為：輸入操作數經過一個加法器后得到加法結果，將加法結果同時傳遞給減法器和比較器，分別得到減去模值和與模值比較的結果，將比較結果作為多路選擇器的選通信號對加法器和減法器的輸出進行仲裁后輸出。

Immutable X與加密支付平臺MoonPay合作，支持用戶以法幣鑄造和購買NFT資產:據官方消息，以太坊NFT二層擴容方案Immutable X與加密支付平臺MoonPay合作，已支持用戶使用信用卡或借記卡以法定貨幣鑄造和購買NFT資產。當用戶使用借記卡或信用卡發起NFT鑄幣時，Moonpay將資金保存在卡上，NFT在用戶的錢包地址上鑄造成功后，資金將轉移到相應的合作伙伴錢包中。[2022/12/8 21:31:17]

除了普通加法和減法操作相結合的方式外，還可以只通過兩次普通加法實現同樣的模加功能，具體的算法定義如下：

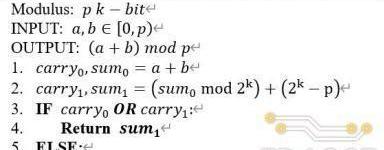
其對應的硬件電路結構由兩個加法器和一個多路選擇器組成，如上圖(b)所示，具體數據通路為：輸入操作數經過第一個加法器，輸出兩數之和與進位；兩數之和繼續輸入第二個加法器(2k?p)與相加后得到對應的和與進位；將兩次加法的進位進行或運算后，作為多路選擇器的選通信號對兩次加法的和進行仲裁后輸出。

上述兩種模加的實現方式，均需要兩個加/減法器，分別完成加法和取余的計算步驟，然后經過一個多路選擇器仲裁后輸出。而不同之處在于仲裁器選通信號的產生方式，第一種算法的選通信號需要通過一個比較器產生，而第二種算法只需要對兩次加法的進位進行一次或運算。相比普通的位運算，比較器在電路實現上通常會消耗大量的硬件邏輯資源，同時產生長的組合邏輯路徑延遲，對電路的時序性能產生不利的影響。尤其是對于Poseidon中255位的操作數，比較器帶來的硬件和時序上的開銷對整體模加電路的影響會更加顯著。因此，TRIDENT中采用了第二種模加算法進行電路設計。

在具體的電路實現過程中，由于Poseidon操作數位寬為255比特，在代碼中直接通過加法符號實現單周期加法器會對整體的時序產生較大的影響。為了提高電路的工作頻率，我們將圖(b)中兩個255比特加法器進行了全流水線化，每個加法器進行五級流水線的分割，并在多路選擇器的輸出端添加一級寄存器，使得整體模加電路總共包含11級流水延遲。流水線化后的模加電路結構如上圖(c)所示。

4.2模乘電路的設計

和模加電路類似，模乘的實現也可以分解成一次普通的乘法運算和取余兩個步驟。這兩個步驟分別對應模乘實現過程中的兩個難點。

首先，從普通乘法的角度，Poseidon哈希函數的操作數的位寬為255Bit，而對于高位寬的乘法器電路，如果實現方式不當，通常會消耗大量的邏輯資源，同時對電路的時序性能造成很大的影響。在實際硬件代碼編寫中，一般不會直接通過乘號實現乘法電路，通常的做法是調用現成的乘法器IP，或者，基于各種優化算法和結構，如Booth編碼和華萊士樹結構等，在電路級層次自行設計乘法器。TRIDENT項目的實現方式為：將高位寬乘法分解成若干并行的小位寬乘法，小位寬乘法則可以通過XilinxFPGADSP模塊中嵌入的28*16的乘法器實現。因此，整個255-Bit高位寬乘法器實現的關鍵在乘法的拆分算法上。

最簡單的拆分方式是基于經典的級聯算法實現，每次拆分將一個乘法器分解為四個并行的位寬減半的乘法器。對于256-Bit乘法器，經過四次遞歸的拆分，可通過256個16-Bit的乘法器實現。這種拆分方式雖然實現的電路結構簡單規整，但拆分后乘法單元的數量仍然不夠理想。TRIDENT中采用了Karatsuba-Ofman算法進行乘法器拆分，這種分解方式雖然在電路結構上相對復雜，并且需要引入額外的加法器，但每次分解只需要三個位寬減半的乘法器，對于256-Bit乘法，三次拆分后總共只需要81個16比特乘法器，大概是普通級聯算法的三分之一。Karatusba-Ofman算法定義如下：

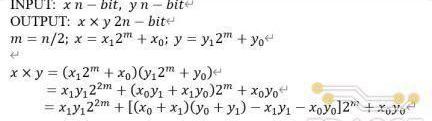
上述算法所對應的乘法器拆分結構如下圖所示，每次拆分后乘法器位寬減半，但數量上增加兩倍，同時需要引入額外的加/減法器。基于遞歸的思想，圖中的三個乘法器還可以不斷地進行拆分，直至位寬滿足需求。TRIDENT項目中對255比特的乘法器進行了三次拆分，最終分解為27個并行的34-Bit乘法器。而34比特乘法器則通過調用Xilinx提供的乘法器IP實現，每個34比特的乘法器IP由4個DSP模塊中乘法器組合而成，因此，一個255-Bit乘法器總共需要消耗108個DSPslices。

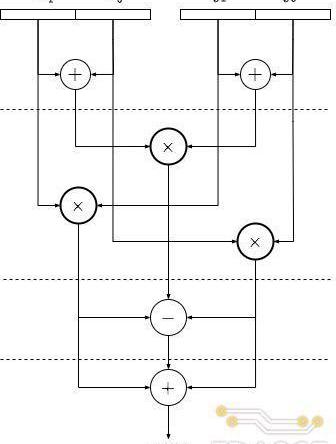
為了提升乘法器的工作頻率，Poseidon加速器中對Karatsuba乘法器拆分架構進行了流水線處理，上圖中的虛線代表一級寄存器，每進行一次拆分乘法器內增加3級流水，而最底層的Xilinx乘法器IP內共有5級流水。因此，255-bit的乘法器經過三級拆分后總共的流水線級數為14。

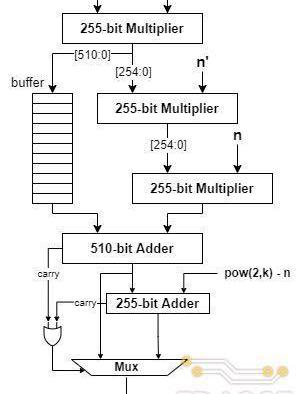
其次，從取余的角度，和模加中通過減/加法即可實現不同，模乘運算的取余通常需要在除法的基礎上完成，而除法器需要復雜的電路結構同時會消耗大量邏輯資源，對于硬件實現不夠友好。因此，大部分模乘電路的設計都采用了優化的取余方式，將除法轉換成其他容易在硬件上實現的算術運算。TRIDENT項目中基于MontgomeryReduction算法實現模乘器電路。Montgomery算法的基本思想是通過數域轉換的方式，將操作數和運算結果轉換到Montgomery域內，在該數域內取余的除法操作可以簡化成移位運算。具體的數域轉換方式為:當模運算的模數為p時，輸入操作數a和b所對應的Montgomery域內的取值為：

a′=a?Rmodp

b′=b?Rmodp

其中R需要滿?R=2k>p;且R和p滿?互質關系，即gcd(R,p)=1;在該數域內的乘法，即Montgomery乘法操作的定義如下：

c′=a′?b′modp

詳細的算法實現流程如下：

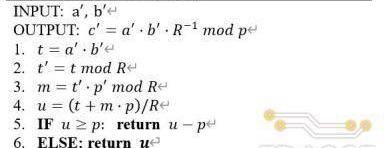
由R=2k可知，上述算法中2-4步的取余和除法操作均可以由移位代替，而在R和p固定的情況下步驟3中p′的值可以提前計算，?5-6步的取余操作可以通過?次加法或減法實現，因此，整個Montgomery模乘算法總共需要完成三次乘法和兩次加法/減法。在具體的電路設計中，為了提?模乘器性能，TRIDENT采?了展開的設計思路，三次乘法運算分別由三個級聯的乘法器完成，使得每個周期均可以輸出?個乘法結果，同時基于流水線技術對長組合邏輯路徑進行切割以使電路達到更高的工作頻率，具體的電路實現結構如下圖所示。

4.3加速器架構設計

在上述單元運算電路的基礎上，實現高性能算法加速器的另一個關鍵在于設計一個高效的電路架構，即如何組織好每一個運算器，最大化每個單元的利用率。

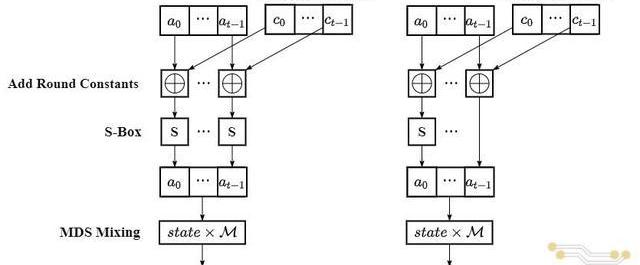
由本文第二部分的介紹可知，TRIDENT所加速的FilecoinPoseidon哈希實例的輸入為個有限域元素，每個元素的位寬為255比特。具體的計算流程由

RF次FullRound循環和RP次PartialRound循環組成。兩種循環的計算流程基本相似，都依次包括AddRoundConstant、SBox和MDSMixing三個階段，在這三個階段分別完成常數模加、五次方模冪和向量—矩陣乘法，兩者唯一的區別在于PartialRound在Sbox階段只需要完成中間狀態第一個元素的計算。FullRound和PartialRound每次循環/迭代的計算流程如下圖(a)和(b)所示。如果將Poseidon哈希函數的所有循環都依次展開，可以將其看成是一條單向的數據流，在該數據流上不斷地進行模加、模冪和矩陣運算。

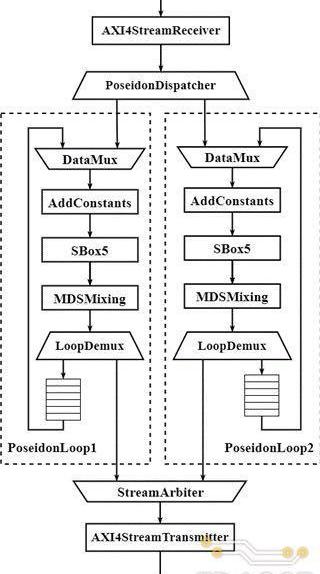
基于上述算法流程的定義，本次課題中實現的Poseidon加速器的具體硬件架構如下圖所示。在Poseidon單次迭代的算法流程的基礎上,加速器的實現針對具體的FPGA架構特點和硬件資源限制做了如下幾點優化：

流水線處理:

為了提高加速器的工作頻率，對Poseidon加速器的數據通路進行了流水線化的處理。數據通路主要由模乘和模加單元組成，而每個模運算單元的組合邏輯路徑都進行了充分的切割，其中模加運算包含了11級流水，而Montgomery模乘器分割成了43級流水，整個計算通路總共由兩百級左右的流水組成。

串行數據處理：

上文提到Poseidon哈希函數中間狀態包含個有限域元素，每個元素的位寬為255比特。在算法流程圖中，中間狀態的所有元素并行地完成每個階段的運算。但在Poseidon硬件加速器的實現中，中間狀態的每個元素串行通過每個硬件計算單元，即一個周期只完成一個有限域元素的計算。而采用串行數據處理方式的主要原因包括：

1.硬件資源的限制：對于Poseidon的MDSMixing階段，如果并行地完成中間狀態向量和常數矩陣的相乘的運算，則需要同時實現個模乘器，其硬件資源的開銷遠遠超過FPGA板卡的限制。

2.輸入數據的形式：Poseidon加速器由XDMAIP提供輸入數據，而XDMA輸出總線位寬為255比特，即每個周期最多只能完成一個有限域元素的傳輸。

3.運算單元利用率：Poseidon中間狀態向量的大小有四種取值，加速器需要兼容不同的大小的中間狀態，而在這種情況下，串行數據處理的方式能夠最大化每個計算單元的利用率。

折疊的設計思路：

Poseidon哈希算法總共由(RP+RF)次迭代組成，對于FilecoinPoseidon實例，根據中間狀態向量大小的不同，總共需要63-65次循環。由于硬件資源的限制，設計中不可能將所有循環都在硬件上展開。因此需要基于折疊的思路，即時分復用的方式，在有限的循環單元上完成Poseidon哈希算法的所有迭代。但同時折疊的實現方式會導致計算性能的下降。因此，如何平衡折疊和展開，從而在有限的硬件資源下達到最好的加速性能，是整個硬件設計的難點之一。TRIDENT中設計的硬件加速器總共實現了兩個并行的Poseidon迭代單元PoseidonLoop，每個PoseidonLoop都可以完成一次PartialRound或FullRound的計算，而整個PoseidonLoop的數據通路呈環狀結構，輸入數據在環中不斷的流動，直至所有迭代完成后輸出。

基于上述架構設計，整個Poseidon加速器的工作流程主要可以分成三個階段：

1.輸入階段:AXIStreamReceiver模塊接收XDMAIP以AXI-Stream總線協議傳送來的輸入數據，并將其轉換成加速器內部的數據傳輸格式。PoseidonDispatcher負責將AXIStreamReceiver輸出的數據分發到兩個迭代單元中。

2.計算階段：輸入數據在兩個PoseidonLoop的環形數據通路中不斷流動，直至所有循環完成后輸出；

3.輸出階段：StreamArbiter對兩個迭代模塊PoseidonLoop的輸出進行仲裁后傳遞給AXIStreamTransmitter模塊，而AXIStreamTransmitter模塊負責將內部數據傳輸格式轉換成AXI4-Stream總線形式輸出。

性能測試

在上文中介紹的FPGA硬件系統和其中Poseidon加速器IP的基礎上，我們通過Vivado集成開發環境將其實現在了VariumC1100FPGA加速卡上，該板卡搭載了XilinxVirtexUltraScale+系列的FPGA芯片，具體芯片型號為具體型號為XCU55N-FSVH2892-2L-E。整個硬件系統實現(Implementation)后的報告以及計算性能的測試結果如下：

5.1VivadoImplementation報告

整體硬件加速系統綜合實現后邏輯資源消耗情況如下表所示：

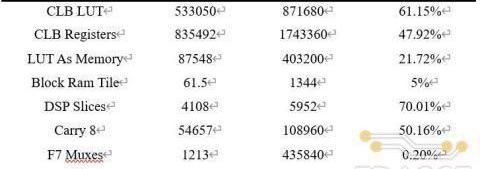
各項FPGA資源中DSPSlices(70.01%)和LUT(61.15%)的消耗最多,主要用于255-BitMontgomery模乘電路的實現上。這兩項資源的不足也限制了在加速器中配置更多模乘器來提升計算并行度和整體的加速性能。

在時序上，實現(Implementation)后Poseidon加速器剛好能夠滿足100MHz工作頻率的要求。關鍵路徑上，建立(setup)時間的余量為0.069ns，保持(hold)時間的余量為0.01ns。

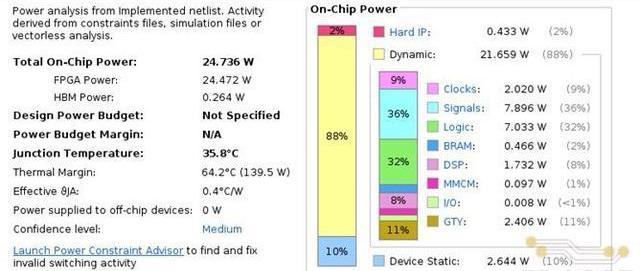
除了資源和時序外，FPGA實現后的功耗信息如下圖所示。由下圖可見，在運行我們設計的加速器硬件時，FPGA芯片的整體功耗在24.7W左右。而我們在性能測試中使用的RTX3070GPU加速卡的運行功耗在120W左右。

5.2計算性能測試

TRIDENT項目中設計了兩種方式測試Poseidon加速器的計算性能：

1.C語言程序測試結果：在Xilinx提供的XDMA驅動的基礎上使用C語言編寫簡單的性能測試程序。該測試程序向FPGA加速器寫入一定數量的輸入數據，并記錄加速器完成所有數據哈希運算所需要的時間。基于該測試程序，我們分別測試了Poseidon加速器在三種長度輸入數據下的性能表現。當輸入數據的大小為arity2,即中間狀態向量元素個數時，加速器在0.877秒內完成了850000次的哈希運算，數據吞吐率可達到29.1651MB/s,即每秒大約能夠完成1M次哈希運算

2.Lotus-Bench測試結果：Lotus中提供了計算機硬件在Filecoin計算負載下性能表現的基準測試程序Lotus-Bench；與自己實現的C語言測試程序相比，Lotus-Bench的測試更加接近實際的工作負載，能夠得到更加準確的測試結果。在Lotus-Bench的基礎上，我們分別測試了CPU,GPU和FPGA在preCommit階段(該階段主要完成Poseidon哈希函數的計算)處理512MB數據所需要的時間。FPGA在Lotus-Bench測試下的算力可達到15.65MB/s，大約是AMDRyzen5900XCPU實現的2倍，但和RTX3070GPU的加速性能相比仍有很大的提升空間.

總結

TRIDENT項目旨在為Filecoin分布式存儲系統中涉及的Poseidon哈希計算實例提供一套完整的FPGA加速方案。硬件上，我們基于XilinxVariumC1100FPGA板卡搭建了一個完整的加速系統，該系統主要由XDMA、FIFO以及Poseidon加速器IP三部分組成，并通過PCIe接口與服務器主機進行數據傳輸。軟件上，我們為Filecoin的具體軟件實現Lotus提供了訪問底層FPGA加速器的接口，并通過Lotus-Bench對加速器的計算性能進行測試和比較。

整個硬件加速系統的核心模塊—Poseidon加速器IP的設計主要可以分成單元運算電路和整體架構兩個部分。其中單元運算電路包括255-Bit的模乘和模加，對于模加器，TRIDENT中采用基于加法的取余方式避免了多余的比較器電路開銷。對于255-Bit模乘電路，我們基于Karatsuba-Offman算法將高位寬的乘法分解成若干并行的小乘法器實現，同時采用MontgomeryReduction算法將取余過程中復雜的除法運算轉換成乘法實現。在加速器架構的設計上，我們針對具體的FPGA硬件資源限制，基于流水線和折疊技術設計了一個串行的Poseidon計算架構。性能表現上，目前FPGA加速器電路能夠工作在100MHz并為Filecoin提供兩倍于AMDRyzen5900X處理器的加速性能。但和RTX3070GPU相比還存在2~3倍的差距，仍然有較大的提升空間。

TRIDENT項目后續的主要目標仍然是繼續優化加速器的計算性能。根據已有的開發經驗，我們認為整個加速系統未來的性能優化可以主要分成三個部分：

1提高電路的工作頻率，包括優化電路設計中高扇出的信號以及長的組合邏輯路徑；

2實現性能-面積比更高的模乘單元：模乘是Poseidon哈希函數中最主要的運算，同時對硬件資源的需求量也是最大的。如果在保持性能不變的情況下，減少模乘電路的硬件消耗，從而在FPGA設計中加入更多的模乘單元，可以進一步提高計算的并行度。

3優化加速器架構：由于需要適配FilecoinPoseidon計算實例中不同大小的輸入數據，目前在輸入較小的情況下加速器中存在一些冗余的運算單元。通過進一步優化加速器的整體架構，使得在不同長度的輸入數據下，所有運算單元都能得到更好的利用，能夠進一步提升整體的加速性能。

Tags：FPGFilecoinDENTFPG幣FPG價格Filecoin幣是什么幣DENT價格DENT幣

ICP