TRA:數字簽名：基于橢圓曲線的簽名方案

在數字時代中，數字化文檔的認證性、完整性和不可否認性，是實現信息化安全的基本要求。數字簽名則是滿足上述要求的主要方式之一，亦是現代密碼學的研究內容之一。

數字簽名有哪些形式？基于密碼學的數字簽名優勢幾何？有哪些常用的數字簽名實現方案？使用過程中又潛藏何等風險？我們將先從理解概念為始，再為大家逐步深入介紹。

區塊鏈百科No.34：基于橢圓曲線簽名方案

隨著計算機信息處理能力的不斷提高，對密鑰長度的要求也越來越高，這個問題對于存儲能力受限的系統來說顯得尤為突出。

橢圓曲線密碼體制（ECC）的提出改變了這種狀況，它可以用更短的密鑰提供與其他體制相當的或者更高級的安全，并已成為迄今被實踐證明安全、有效、應用較廣的3種公鑰密碼體制之一。本文將繼續為大家介紹基于橢圓曲線的數字簽名方案。

STEPN數字鞋鑄造總量已超70萬雙:8月4日消息，據Dune Analytics數據顯示，STEPN數字鞋鑄造總量已超70萬雙，截至目前為735,342雙，全生命周期用戶量達到943,531個。STEPN過去7天活躍用戶量達到34,309，新鑄造數字鞋6,462雙。[2022/8/4 5:15:31]

橢圓曲線在代數學和幾何學上，已被廣范研究了150年之久，有堅實的理論基礎。

所謂橢圓曲線是指維爾斯特斯拉（Weierstrass）方程：

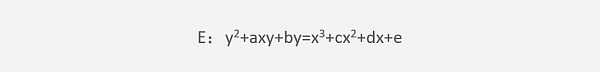
所確定的平面曲線，其中a、b、c、d、e屬于域F，其可以是有理數域Q、復數域C，還可以是有限域GF（p）。

重慶紅巖革命歷史博物館限量發布首款數字藏品:金色財經報道，據消費日報網消息，重慶紅巖革命歷史博物館限量發布首款數字藏品—《紅巖石碑》，這款帶有歷史紀念意義的數字藏品《紅巖石碑》受到了廣大民眾的喜歡和支持，上線2小時58分后2999件藏品全部搶空。[2022/6/17 4:33:51]

橢圓曲線是其上所有點（x、y）的集合，外加一個無窮遠點O（定義橢圓曲線上一個特殊的點，記為O，它為仿射平面無窮遠的點，稱為無窮遠點。在xOy平面上，可以看做平行于y軸的所有直線的集合的一種抽象）。

密碼學中普遍采用的是有限域上的橢圓曲線，它是指橢圓曲線方程定義式中，所有的系數都是在某一有限域GF（p）中的元素。它最簡單的公式為：

日本前內閣府副大臣：當前數字貨幣市場法規仍不完善:近日，日本前內閣府副大臣Minukiuki Fuku參與活動表示，盡管當前數字貨幣市場上的法規有很多不清楚的地方，但這是新興市場規則形成過程中所必不可少的。然而在實際參與制定數字貨幣市場的規則中面臨各種障礙，遇到的第一個問題就是如何稱呼除比特幣外存在的虛擬貨幣。[2020/10/26]

該橢圓曲線上只有有限個離散點，設為N，則N稱為橢圓曲線的階為N。N越大，安全性越高。基于此，橢圓曲線的圖示可以表示如下：

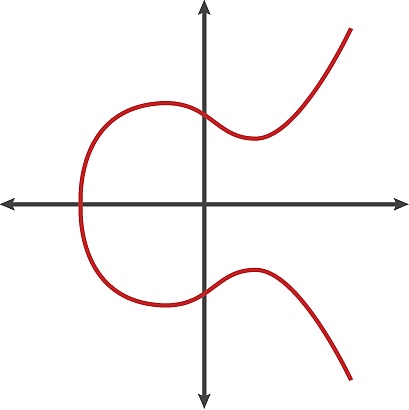
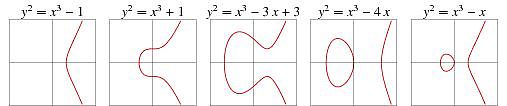
當然，基于不同變量值，橢圓曲線還有其他的表示形式：

金沙江數字基金：“投資界”報道失實 已投資IPSE分布式搜索項目??:3月12日，“投資界”發表標題為《金沙江創投緊急聲明：我們沒投過這家公司》的文章，文中出現多處針對伍伸俊、金沙江數字基金的誹謗、混淆和誤導性言論，如金沙江數字基金投資IPSE是“騙局”，“硬頂著創始人名號，誤導投資虛擬貨幣”等，是對伍伸俊極大不尊重，造成了極其惡劣的影響。為澄清事實，金沙江數字基金嚴正聲明：投資IPSE分布式搜索項目的是金沙江數字基金而非金沙江創投。金沙江創投與金沙江數字基金除創始人同為伍伸俊之外，無其他任何實質性聯系。如再出現相關誹謗、污蔑和混淆視聽行為，金沙江數字基金將依法追究其責任。[2020/3/15]

當我們仔細觀察這些曲線時，能發現一些有趣特性：（1）對稱性，即曲線上的任何一點都可以在x軸上反射，并保持曲線不變；（2）任何非垂直直線與曲線的交點至多有三個。

動態 | Finacle Trade Connect將幫助哈頓國家銀行將業務流程數字化:據bitcoinexchangeguide報道，斯里蘭卡哈頓國家銀行（HNB）選擇Finacle Trade Connect來監督區塊鏈驅動的跨境和國內貿易融資網絡。據悉，該銀行是斯里蘭卡領先的私營商業機構之一。Financle Trade Connect將協助該行業務流程的數字化，例如重要文件的認證和驗證，同時運營可信、共享和分布式網絡。[2019/3/16]

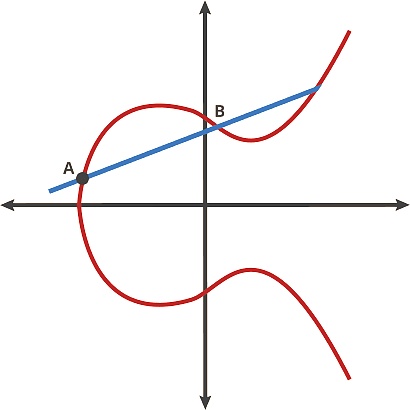
我們可以把這條曲線想象成一場桌球游戲。在曲線上取任意兩點并通過它們畫一條直線，它將與曲線相交于另一個位置。在這個桌球游戲中，你在A點拿一個球，把它射向B點，當它擊中曲線時，球要么直接向上反彈(如果它在x軸以下)，要么直接向下反彈(如果它在x軸以上)到曲線的另一邊。我們可以把球看做在兩個點間移動，曲線上的任意兩點碰撞可得到一個新的點。

A·B = C

或者可以用某一個點自身不斷碰撞出新的點。

A·A = B

A·C = D

……

在這個過程中，一個初始點經由n次運算會得到最后到達的點，當你只知道這兩個點的值，要找出n是很難的。

這就像一個人在房間里隨機玩一段時間桌球游戲，對他而言，按照上面描述的規則一遍又一遍地擊球是很容易的。但如果有人走進房間，球剛好結束到達一個點，即使他知道所有的游戲規則，以及球從哪個點開始，也不能確定球到達此處所被擊中的次數。容易正向計算，難以反向計算，這也是陷門函數的基礎。

1985年，Koblitz和Miller將橢圓曲線引入密碼學，提出了基于有限域GF（p）的橢圓曲線上的點集構成群，在這個群上定義離散對數難題并構造出基于其的一類公鑰密碼體制，即基于橢圓曲線的離散密碼體制，其安全性基于橢圓曲線上離散對數問題的難解性。

我們以基于橢圓曲線的ECDSA數字簽名實現方案為例，闡述其具體的實現過程。

密鑰生成算法

假設GF（p）為有限域，E是有限域GF（p）上的橢圓曲線。選擇E上一點G∈E，G的階為滿足安全要求的素數n，即nG=O（O為無窮遠點）。

選擇一個隨機數d，d∈[1，n-1]，計算Q，使得Q=dG。那么公鑰為（n，Q），私鑰為d。

簽名算法

假設待簽名的消息為m，經過如下計算過程，簽名者對消息m的數字簽名為（r，s）。

驗證算法

簽名接收者B對消息m簽名（r，s）的驗證過程如下：

判斷r和r1的關系，如果相等，則簽名有效；否則，簽名無效。

除了上述介紹ECDSA方案之外，基于橢圓的數字簽名方案還有很多，而類似DSA的其他方案例如Schnorr、EIGamal等方案也都被移植到橢圓曲線有限群上。

從上述介紹可知，數字簽名的安全性依賴于基于橢圓曲線的有限群上的離散對數難題。

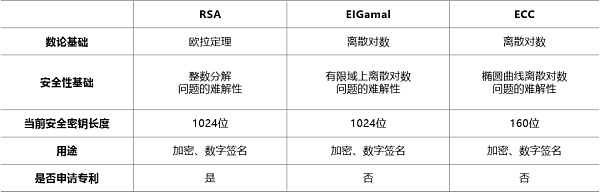
與前章所述RSA數字簽名和基于有限域離散對數的數字簽名相比，基于橢圓曲線的數字簽名方案具有如下特點：在相同的安全強度條件下，簽名長度短，密鑰存儲空間小，適用于存儲空間有限，帶寬受限、要求高速實現的場合。

此外，橢圓曲線資源豐富，同一有限域上存在著大量不同的橢圓曲線，這也為安全性增加了額外的保障。

正是由于橢圓曲線具有豐富的群結構和多選擇性，并可以在保持和RSA、EIGamal體制同樣安全性的前提下大大縮短密鑰長度，因而有著更為廣闊的應用場景。

Tags：TRASTEPFINAConnectTRANSstepn幣價Finance BlocksConnectome

幣安幣