PLO:學習筆記 | 零知識證明算法之PLONK——協議

上一篇主要描述了PLONK協議里的一個核心部分，用置換校驗的方法去證明電路門之間的一致性；接下來，將繼續分享如何證明門的約束關系得成立，以及整體的協議剖析。

門約束

舉個簡單的例子，假如存在一個電路，電路中僅有3個乘法門，對應的約束如下：

L1*R1-O1=0

L2*R2-O2=0

L3*R3-O3=0

進行多項式壓縮：定義多項式函數L(X),R(X),O(X)滿足：

L(1)=L1,R(1)=R1,O(1)=O1

L(2)=L2,R(2)=R2,O(2)=O2

L(3)=L3,R(3)=R3,O(3)=O3

此時，定義新的多項式函數F(X)，令F(X)=L(X)*R(X)-O(X)

則有：

F(1)=L(1)*R(1)-O(1)=0

F(2)=L(2)*R(2)-O(2)=0

F(3)=L(3)*R(3)-O(3)=0

也就是表明：如果多項式函數F(X)在X=1,2,3處有零點，則說明門關系約束成立。

多項式函數F(X)在X=1,2,3處有零點則表明多項式F(X)可以被(X-1)(X-2)(X-3)整除，為了和論文一致，我們把這個多項式函數設置成Z(X)，即：

iExec 與微軟 Azure達成合作，利用 SGX 來保護機器學習代碼和數據:11月5日消息，分布式云計算平臺 iExec 云算寶與微軟云計算平臺 Azure 就發展“機密計算”達成合作伙伴關系，iExec 利用英特爾軟件防護擴展（SGX）來保護機器學習中的敏感代碼和數據。iExec 信息安全總監 Zhang Lei 談到：Azure 機密計算通過保護使用中的數據有效地解決了安全問題。iExec 利用英特爾 SGX，使珍貴數據在廣泛共享和使用的同時，還能保護其隱私和所有權。iExec 將這些獨特的功能結合在一起，使人工智能開發者能夠保護他們的知識產權，同時為人工智能開發者創造新的經濟機會。[2021/11/5 21:28:36]

F(X)=T(X)*Z(X)==>T(X)=F(X)/Z(X)

如果能證明T(X)是一個多項式，則說明多項式F(X)與Z(X)有相同的零點，進而說明門約束關系成立。

一般過程應該如下：

1.P計算F(X)并把F(X)發送給V；

2.V根據Z(X)直接校驗F(X)/Z(X)

但是如此過程存在兩個問題，一個是復雜性問題，假如F(X)的階為n，那通信復雜度就是O(n)；而是安全性問題，多項式F(X)完全暴露給V。

那應該如何解決這兩個問題呢？最佳的答案可能就是：多項式承諾

學習時報：區塊鏈等信息化工具在疫情防控中發揮重要作用:學習時報發文表示，在中國的疫情防控中，有效發揮了人工智能、大數據分析、機器人、北斗系統、健康碼、區塊鏈、智慧城市、無人機等信息化工具的作用，充分彰顯了科技向善的力量，這些經驗可與世界交流借鑒。我們應集中全球科學資源，與世界知名的制藥公司、研究機構加強科技交流，聯合加強疫苗、藥物、快速檢測試劑盒研究研制。[2020/3/20]

多項式承諾

什么是多項式承諾？就是證明方P用一個很短的數據來代表一個多項式F，這些很短的數據可以被驗證方V用來驗證多項式F在某一點的值確實為證明方P聲稱的值z。

具體看一下論文里的定義：

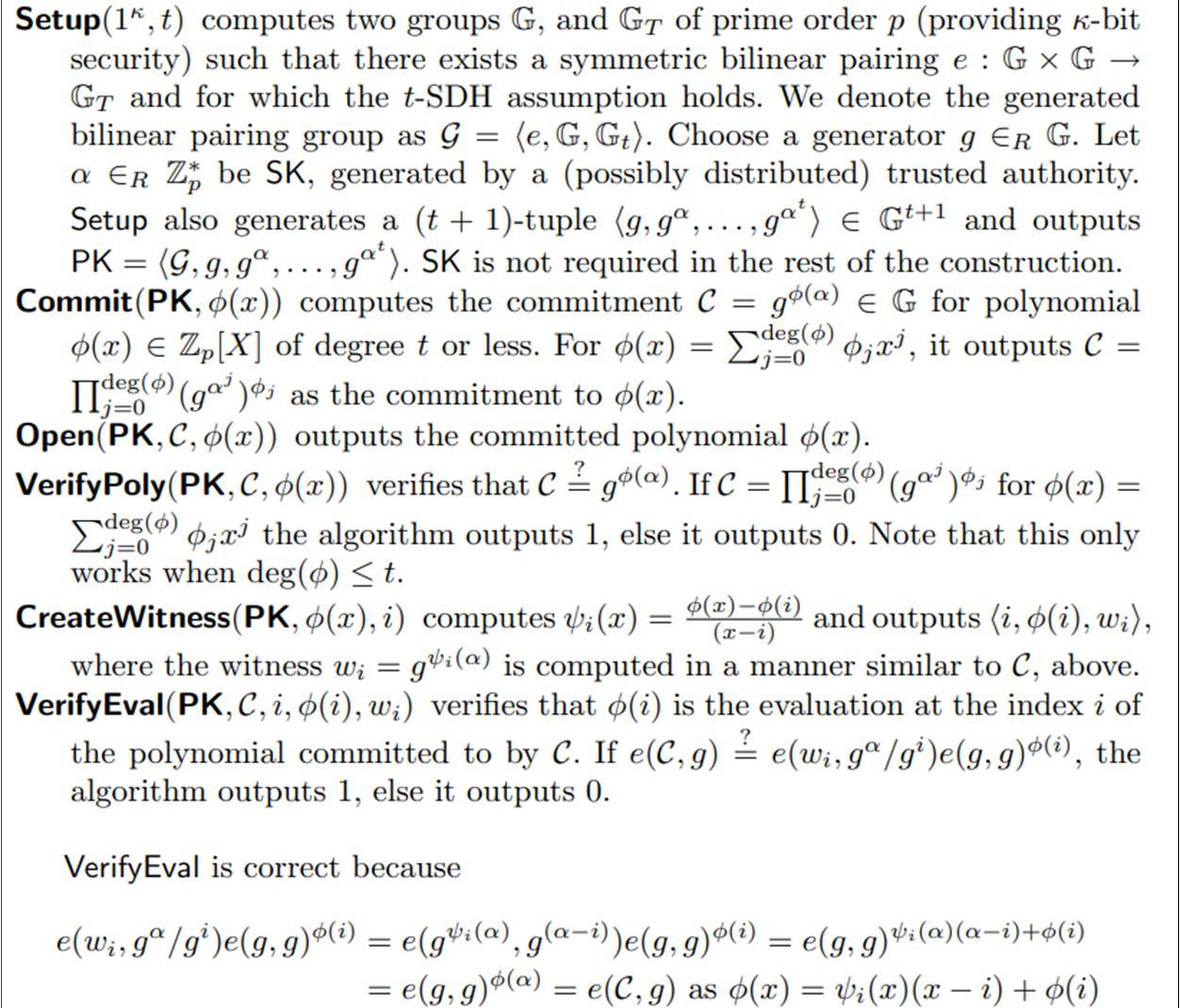
由圖可知：

1.Setup:初始化，生成計算多項式承諾需要的一些必備參數；

2.Commit:計算多項式承諾，其結果是一個值；

3.Open:返回與多項式承諾對應的多項式函數；

4.VerifyPoly:驗證多項式承諾是否和多項式函數一致；

5.CreateWitness:證明多項式函數在某一點的值是否是證明方P聲稱的值，具體的數學方法就是：判斷多項式是否能被整除，即：

聲音 | 江卓爾：熊市宜早睡、健身、屯幣、裝死、反省、學習、練內功、少折騰:萊比特礦池江卓爾發微博稱，熊市宜早睡、健身、屯幣、裝死、反省、學習、練內功、少折騰。[2018/12/28]

6.VerifyEval:驗證方V驗證多項式函數在某一點的值是否是證明方P聲稱的值，具體的數學方法是：利用雙線性配對驗證其數學乘法邏輯關系。

繼續回到我們上面的問題：

證明方如何證明：T(X)=F(X)/Z(X)，我們再簡化一下場景，就令Z(X)=X-1，則:

T(X)=F(X)/(X-1)==>T(X)*(X-1)=F(X)==>T(X)*X=F(X)+T(X)

對應多項式承諾的協議可知：證明方P其實是想證明多項式函數F(X)再X=1處的值為0，因此根據協驗證方只需要證明：

e(Commit(T(x)),x*G)=？e(Commit(F(x))+Commit(T(x)),G)(雙線性配對的性質)

可以看出，利用多項式承諾的數學工具，既可以實現復雜度的優化，又可以實現隱私保護。

協議

接下來分析一下完整的PLONK協議：

Relation

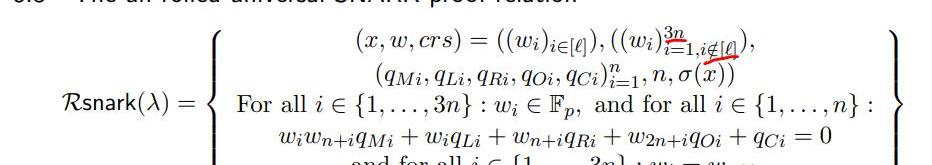
加密貨幣投資人暴走恭親王：加密貨幣的投資，需要花時間學習和了解項目:今日凌晨，著名加密貨幣投資人暴走恭親王發布微博，稱：對于新人而言，我個人的建議是利用這段時間可以多學習行業的知識，我始終認為你只有對行業越了解，你才能對于行業越有信心。如果你對數字貨幣不了解，對參與的項目不了解，對全球發展趨勢不了解，那么群里只要有一些風吹草動，你馬上就會心中生出無數的疑慮，并且很快會在謠言中作出很多讓你可能抱憾終身的決定（這種決定我也做過）。很多人希望在群里面充值信仰，我個人覺得很難，如果你真的能夠把時間花在學習和了解知識以及項目上，那真的可以讓你握住自己的幣。發文疑似是對周末“過山車”行情的觀點表達，他也表示發文是“關于幣本位和充值信仰”。[2018/3/19]

上圖表示了PLONK算法里，要證明的一種關系，需要說明的是：

1.w代表著電路里的輸入、輸出，總共3n個，n是電路里乘法門的數量，每個門都有左輸入，右輸入和輸出，因此w總共有3n個；

2.q*代表著選擇向量，它的取值對應這這個是乘法門，還是加法門等類似的約束類型

3.σ代表著置換多項式，其表示門之間的一致性約束索引

4.倒數第一個公式代表門之間的約束成立

5.倒數第二個公式代表門的約束關系成立

CRS&P_Input&V_Input

Algorithmia公司推出基于區塊鏈的機器學習合約DanKu:算法公司Algorithmia于本周二推出了基于區塊鏈的機器學習合約DanKu。DanKu是一個可以評估被提交模型的神經網絡，以太幣獎勵獲勝者。[2018/3/1]

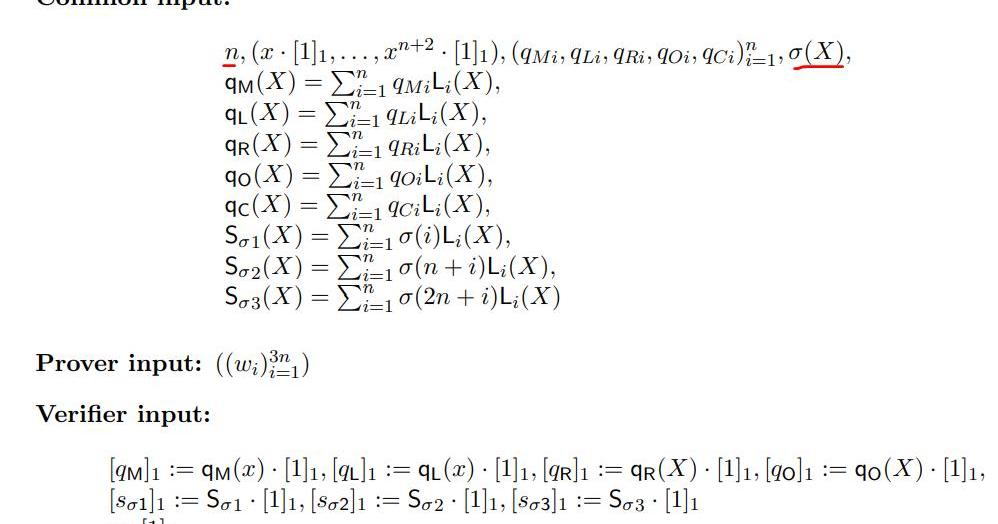
上圖表示了PLONK算法里的CRS設置，以及證明方P和驗證方V的一些輸入，需要說明的是：

1.整個協議都是基于多項式的，因此需要構建對應的多項式形式。

2.多項式σ的階是3n的，由于和多項式承諾相關的CRS最高的階位n+2，因此需要把σ拆分成3個多項式S,分別記錄每個多項式的置換關系(L,R,O);

3.為了減少通信復雜度和保護隱私，協議基于多項式承諾構建，因此驗證方V的輸入都是承諾值。

Prove

上圖表示了PLONK算法里證明方的一些操作，需要說明的是：

1.b1,...b9是隨機數，從用法看是為了安全，但是我暫時也沒明白，不加這個隨機數，又會有什么安全問題？

2.a(X),b(X),c(X)分別是代表了電路里的左輸入，右輸入和輸出

3.,,表示多項式的承諾值，參考多項式承諾小節里的承諾計算方法

上圖表示了PLONK算法里證明方的一些操作，主要是置換校驗，參考第一篇的置換校驗的協議過程，生成多項式z(X)，需要說明的是：

1.β和?都是用來生成置換校驗函數的參數，詳見第一篇里f`(x)和g`(x)的生成過程；

2.z(X)的生成方式對應置換校驗里跨多項式的生成過程，Li(X)為拉格朗日多項式基，性質滿足，盡在x=i的時候為1，其他為0；

3.注意區分ω和w，ω是群H的生成元，是多項式的自變量的取值。w是電路的左輸入，右輸入和輸出，是多項式L,R,O在在群H上的取值。

上圖表示了PLONK算法里證明方P的一些操作，主要是把門約束和門之間的一致性約束組合到一起，通過α，需要說明的是：

1.根據前面的描述，門約束多項式和一致性約束多項式在群H上的所有元素都是取值為0的，因此都會被多項式ZH(X)整除，等同于上面所述的T(X);

2.因此，證明方只要能證明整除的結果的確是多項式，那就能證明，門約束多項式和一致性多項式在群H所有元素上取值為0，即所有約束關系成立，即電路邏輯成立；

3.可以知道的是t(X)的階最高為3n，但是用于計算承諾的CRS只到了n的級別，因此需要把多項式t(X)拆分，然后單獨計算承諾值。

上圖表示了PLONK算法了證明方P的一些操作，主要根據多項式承諾的協議，前面P算出了多個多項式在點x=z處的值是多少，現在要用多項式承諾協議去證明，這些計算是正確的，需要說明的是：

1.為了減少驗證方V的操作復雜度，t(X)的分子部分r(X)在x=z處的值，P計算好，然后驗證方直接驗證，其他的操作類似；

2.v的值看起來是為了更安全；

3.Wz(X)對應多項式協議里的CreateWitness操作，證明這些多項式r(X),a(X),b(X)等在x=z處的值確實等于r,a,b等，對Wzw(X)同理，并返回承諾值。

Verify

至此，證明方P的所有操作都完事了，接下來都是驗證方V的操作。

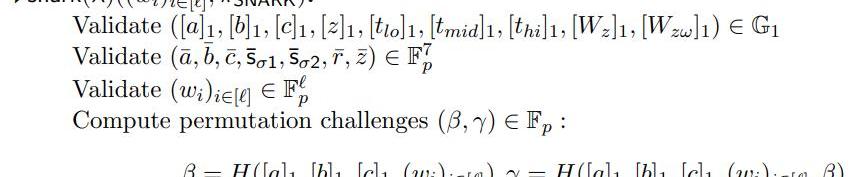
上圖表示了PLONK算法里驗證方V的一些操作，主要重新生成相關的參數，確保證明方P沒有作惡。需要說明的是：

1.從輸入看，比較清晰，就是一些公開的輸入和證明方P的證明輸出；

2.根據輸入，生成置換校驗過程中需要的一些參數

上圖表示了PLONK算法里驗證方V的一些操作，對于一些公開的，并且計算復雜度很小的多項式，其在x=z處的值還是需要自己計算，更為方便。需要說明的是：

1.根據證明方P的過程來看，驗證方V的核心工作就是驗證兩個多項式承諾；

2.兩個多項式承諾驗證需要兩個配對，可以通過一個參數組合成一個配對，即μ；

3.在驗證前，先計算Wz(x),Wzw(x)的分母在x=z處的值，兩部分，減數和被減數，分別對應,。μ作為系數的，就是對應Wzw(X)多項式的。

4.最后通過一個雙線性配對操作完成兩個多項式承諾的驗證。

結束

至此，PLONK算法的協議原理已全部分享完成，公式很密集，但是細分下來，又很有層次感。能堅持看完，已實屬不易。各位讀者有什么不同的簡介，還請指教，謝謝。

Tags：PLOLONEXEXECPLO價格poloniex兌沖金dexe幣最新消息XEC價格

抹茶交易所