區塊鏈:密碼學技術何以為信？深究背后的計算困難性理論

作者：李昊軒?

來源：

微眾銀行區塊鏈

隱私保護為何選用密碼學算法？密碼學算法背后有哪些神奇的數學理論？3何時比9大？計算可逆性錯覺究竟是如何在數學領域被打破？

這里，我們將從密碼學信任的理論基礎出發，分享在隱私保護技術方案中應用密碼學技術的一些思考：如何理解密碼學算法的能力邊界，如何客觀地比較不同密碼學算法對于隱私保護方案有效性的影響。

這一切，要從密碼學神奇的“不對稱性”說起。

神奇的“不對稱性”

早在公元前，古埃及、古羅馬、古希臘等古文明均已開始使用密碼技術來保護信息的機密性，歷史上最早的不對稱性表現為選用特殊的信息編碼方式，如果第三方不知道具體的編碼方式，則難以解碼對應的信息。

大約經過4000多年的發展，也就是近代20世紀初，現代密碼學正式成型，引入了關于不對稱性更為嚴謹的數學定義。比較有代表性的早期論文包括1929年LesterS.Hill在美國數學月刊上發表的《CryptographyinanAlgebraicAlphabet》。

聲音 | 上海交通大學來學嘉：區塊鏈為密碼學創造了價值:據巴比特消息，上海交通大學教授來學嘉在接受采訪時提到了區塊鏈對密碼學的兩大貢獻。第一大貢獻是為抗抵賴、抗捏造提供了完整的解決方案。區塊鏈能做到抗抵賴，是因為區塊鏈本身就是第三方，參與者自覺服從，數字簽名為抗抵賴提供證據。另外，他還指出了區塊鏈對密碼學的另一個貢獻——區塊鏈為密碼學創造了價值，過去的密碼學是“賠錢”的，因為要用于保護信息系統的安全，增加了開銷；有了區塊鏈后，現在的密碼學是“值錢”的，因為密碼算法的計算結果（coin）具有價值，另外算法本身也具有價值，比如勒索軟件，你要付錢才能解開。[2019/2/25]

20世紀末，隨著因特網的普及，大量敏感數據在網絡上進行傳輸，產生了大量的數據內容保護的需求，密碼學技術也因此得到飛速發展。

在現代密碼學中，關于不對稱性，大家最熟悉的概念莫過于“公鑰”和“私鑰”。

以加密通信為例，主人公小華要向他的朋友美麗通過加密的方式發送一份電子郵件，可以先找到美麗的公鑰，使用公鑰對郵件內容進行加密，并將加密后的得到密文發送給美麗。美麗收到郵件內容的密文之后，通過自己的私鑰進行解密，最終得到郵件內容的明文。

以上過程中，密碼學算法神奇的不對稱性體現在以下問題中：

為什么只有美麗可以解密郵件內容？

為什么其他人不能通過美麗的公鑰反推出她的私鑰？

這些問題的答案，都要歸結于密碼學中的計算困難性理論。

現場 | 姜海：密碼學將隨著黎曼猜想等理論研究的深入迎來大發展:金色財經現場報道，今日，2018可信區塊鏈峰會在北京召開。在主題為“區塊鏈安全焦點關注”的區塊鏈安全論壇上，丁牛科技有限公司CEO姜海結合最近黎曼猜想被證明引起了密碼學界的高度關注，分析了黎曼猜想與區塊鏈密碼安全。他提出，盡管黎曼猜想的證明對于傳統密碼安全有極大的沖擊，但是區塊鏈技術的安全建立在SHA-256、橢圓曲線、算法校驗等基礎之上，在使用過程中能夠極大地抵抗密碼攻擊。盡管最近有很多的安全事件發生，而其根本原因在于程序的違規操作。未來隨著隨機發生器、量子計算機以及黎曼幾個等基礎理論的研究，密碼學將會有更大的發展空間。[2018/10/10]

計算困難性理論

在隱私保護場景中，計算困難性理論具體表現為，對同一隱私數據主體，通過不同計算路徑，獲得相同信息的計算難度具有不對稱性。不對稱性中，相對容易的計算方式被用來構造授權的數據訪問，而困難的計算方式被用來避免非授權的數據泄露。

構造這樣的不對稱性的方式有很多，最經典的方式之一，就是千禧年七大難題之一——P和NP問題。

P問題是確定性圖靈機，即通用計算機計算模型，在多項式時間(O(n^k))內可以計算獲得答案的一類問題。NP問題是確定性圖靈機在多項式時間內可以驗證答案的正確性，但不一定能計算出答案的一類問題。

金色財經現場報道 現代密碼學之父：近幾年是密碼學的又一次復興:金色財經現場報道，今日在Coindesk 2018共識會議上，現代密碼學之父，圖靈獎得主，Cryptic Labs首席科學家Whitfield Diffie表示，最近幾年是密碼學的又一次復興，區塊鏈是密碼學方面的重新對焦。他表示喜歡“引入市場力量”的說法， 從市場力量的角度看待密碼學的發展可能是最好的。Diffie還稱贊了比特幣創始人Satoshi，他說：“多年來密碼學領域的許多人都想到如何發展金錢技術，在Satoshi之前沒有人取得成功。”[2018/5/15]

關于同一份答案，驗證過程比計算過程要容易很多，由此我們可以構造出密碼學算法所需要的計算難度不對稱性。

NP問題是否能夠通過有效的多項式時間算法轉化成P問題，由此破解計算難度不對稱性？目前學術界尚無定論。

理論研究進一步表明，對于NP問題集合中的核心問題，即NP完全問題，如果能夠找一個有效的多項式時間算法來解決任何一個NP完全問題，那其他所有NP問題都可以基于這個算法來構造出有效的多項式時間算法。由此，之前提到的計算難度不對稱性將不復存在。

幸運的是，經過將近70年的科學探索，這樣的算法并沒有被發現。在有限時間內，現代計算機難以求解這些問題的答案，所以現代密碼學可以比較安全地基于這些NP完全問題來構造有效的密碼學算法。

Andrew Miller拜訪Hyper Pay團隊 為該團隊帶來關于密碼學以及更好開發服務安全性的見解 :近日，Andrew Miller 拜訪了全球數字貨幣跨境支付整合平臺Hyper Pay團隊并進行了友好交談。Hyper Pay團隊非常感謝 Andrew 為他們帶來了一些關于密碼學以及更好開發服務安全性的深入見解。 ?[2017/12/19]

神奇的“計算困難問題”

形象地講，計算困難性理論的核心就是構造一個迷宮，如果不知道捷徑，是很難到達出口的。

我們日常所用的各類密碼學算法，其有效性都與這一理論息息相關，這里重點以非對稱密碼學算法為例，介紹其中經典的迷宮構造藍圖，即三大計算困難問題：

大數分解困難問題

離散對數困難問題

橢圓曲線上的離散對數困難問題

大數分解困難問題

給定兩個大素數p和q，計算n=p*q是容易的。然而，給定n，求解p、q則是困難的。

整數的素數分解是數論中最著名的問題之一，目前，求解素數分解最有效的方法稱為數域篩法，即通過構造代數數域不停地對整數可能的集合進行迭代運算。

目前，大整數分解問題仍不存在更有效的分解方法，因此密碼學一些方案利用大數分解困難問題構造相應協議，如RSA系列算法將其困難性規約為大數分解困難問題。如果大整數分解困難問題被破解，使用RSA密碼方案保護的隱私數據也會相應遭到破譯。

斯坦福大學應用密碼學租開發“防彈比特幣”技術:斯坦福大學的應用密碼學組織（ACG）提出一種名為“防彈比特幣”的技術，可以大幅降低區塊鏈數據的大小。ACG團隊稱該技術可以減小交易密碼證明區塊的大小，從原來的10kB縮小到小于1kB，目的在于增強比特幣的保密性，并提高交易速度。[2017/11/20]

離散對數困難問題

在模為n，生成元為g的有限域中，給定整數a，計算g^a=b是容易的。然而，給定b和g計算a則是困難的。

許多新接觸密碼學的讀者都會對離散對數問題產生計算可逆性的錯覺，看起來就是進行一次log運算的事情，但真相并非如此。

在實數域，元素有一個非常重要的性質，全序關系，所以很容易比較大小。例如，在實數域中9>2且3>2，一定能推出9>2。

在計算log2(9)時，計算機會對以元素9為輸入的函數結果進行二分查找法，首先計算(9/2)^2和9進行比較，再計算/2)^2…。通過不停比較元素大小的性質，從而計算log最終的結果。

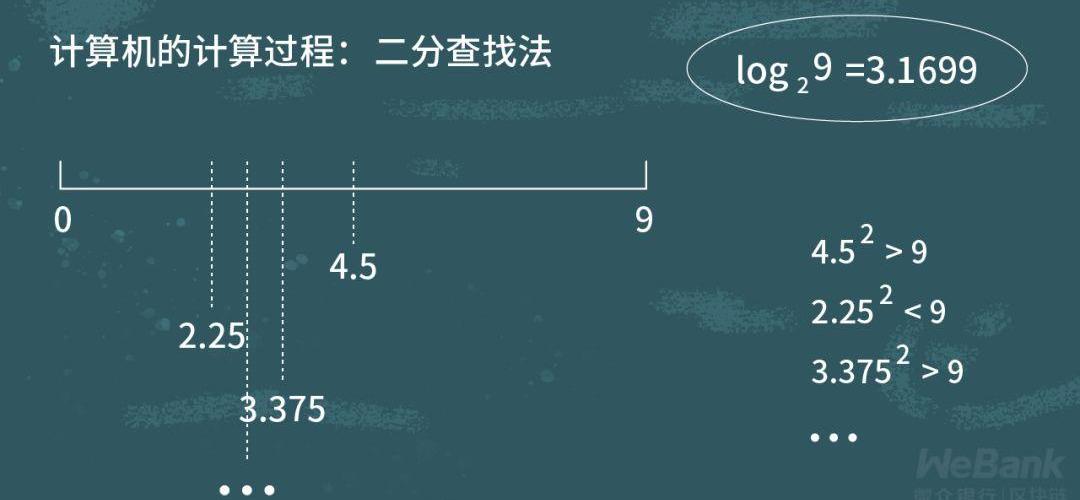
然而，在有限域中，元素之間并不存在全序關系。在模為7的有限域中，可以看到諸如9等于2，3比9大的關系存在。

因此，無法通過有效的算法計算上述過程中的a。許多著名的密碼協議安全性都是建立在離散對數困難性上的，如Diffie-Hellman密鑰交換協議、ElGamal加密、DSA算法等。

橢圓曲線上的離散對數困難問題

當前，橢圓曲線密碼學算法是當前密碼應用的主流，每一個隱私數據都能以坐標(x,y)的形式，表示為橢圓曲線上的一個點。與一般離散對數困難問題類似，橢圓曲線上的離散對數困難問題可以表示為：

在有限域F上的橢圓曲線群，點P為曲線上某個點，給定整數a，計算a*P=Q是容易的。然而，根據P和Q計算a則是困難的。

有別于普通代數運算，橢圓曲線上的點運算定義如下：

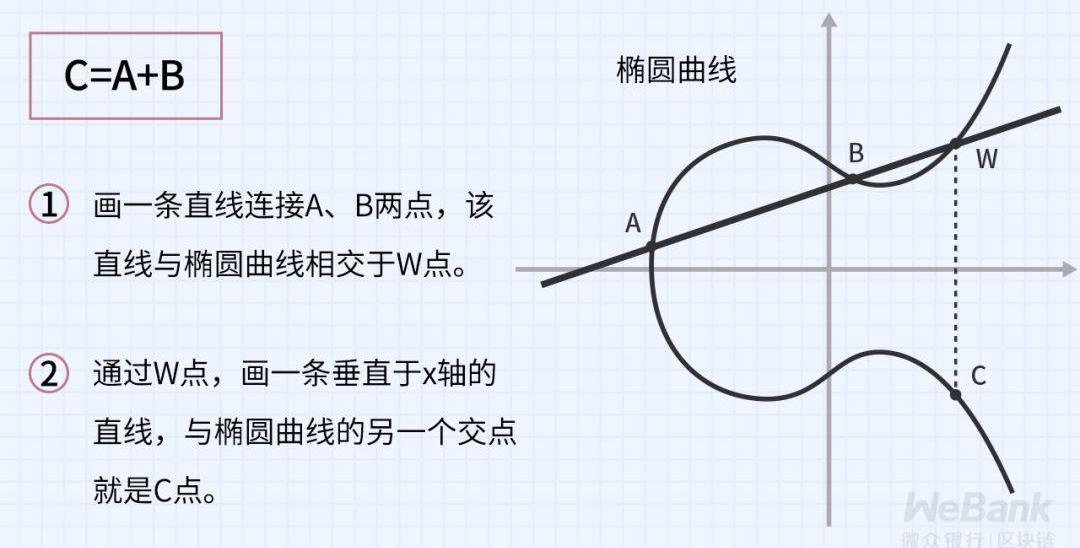
可以看到，橢圓曲線上的點運算和普通實數域上的運算有很大差別，當前尚未存在一種有效的算法對橢圓曲線離散對數問題進行破譯。目前，最常用的公鑰密碼算法體系ECDSA、EdDSA、國密SM2等都是基于這一困難問題。

客觀比較不同的密碼學算法

由于不同的密碼學算法構造使用了不同的困難問題，對應地，不同的困難問題也勢必會引入不同的安全假設。

理解這些安全假設，是企業進行技術選型，客觀地判斷基于不同密碼學算法構造隱私保護方案孰強孰弱的關鍵。

這里，我們需要進一步引入“安全參數”的概念。

安全參數是一個衡量密碼學算法保護隱私數據強度的數值。對位于“同一等級"的安全參數值來說，不同密碼學算法的安全級別基本相同，即面對已知最有效的攻擊方式，算法被破解導致隱私數據泄露的概率相同。

一般情況下，安全參數值的大小，直接體現為密鑰長度的長短。在同一等級下，安全參數值有大有小，對應的密鑰長度也有長有短。

基于不同困難問題的密碼學算法密鑰最小長度，美國國家標準與技術研究院NIST作如下推薦，其中，每個單元格表示需要使用密鑰長度的最小比特數。

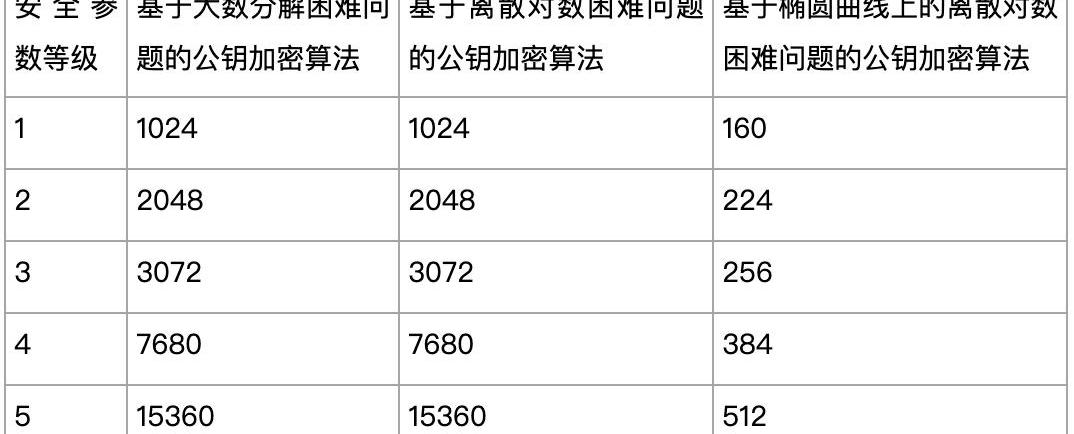
通過上表，我們可以看到，即便密鑰長度相同，選用不同困難問題獲得的安全級別是不同的。一般而言，基于同一困難問題構造的技術方案，密鑰長度越長，安全性越高，相應地，系統效率越低，其中往往也伴隨其他系統設計上的取舍。

不同場景應按照業務需求選擇適合的技術方案和密鑰長度，具體有以下幾點需要特別注意：

隱私保護技術方案的安全性取決于其使用的密碼學算法實現中最低的安全參數等級。

在未指明安全參數的前提下，進行密碼學算法的安全性比較沒有實際意義。

如果安全參數值很小，一般表現為對應的密鑰長度很短時，無論密碼學算法設計多么精妙，實際效果可能都是不安全的。

由于困難問題選用上的差異，密碼學算法的理論強度沒有最強，只有在滿足特定安全假設下的夠強，強行比較基于不同困難問題的密碼學算法哪個更強通常沒有實際意義。

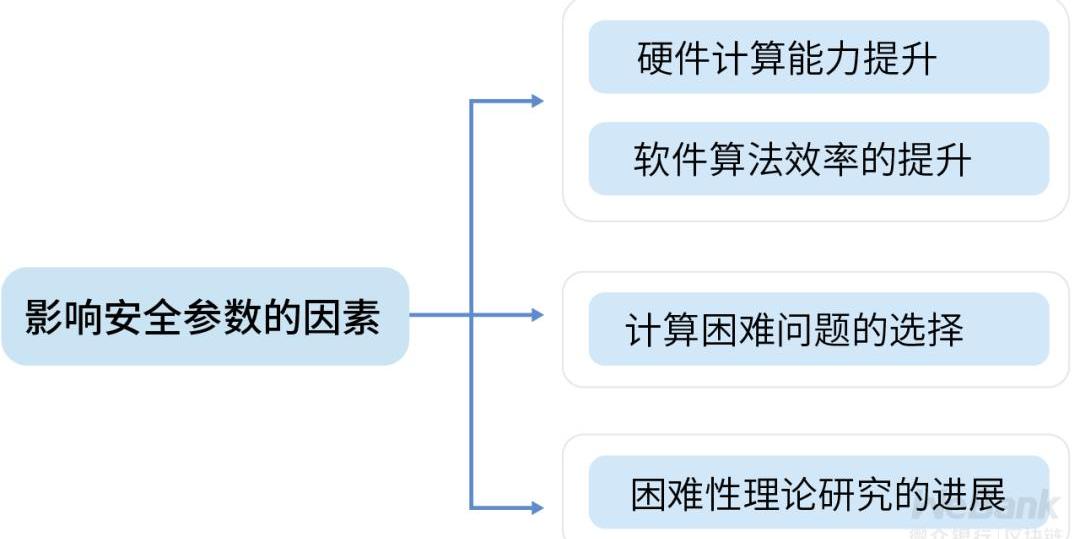
計算困難問題歸根結底還是一個計算問題，隨著計算機計算能力的增強，或是算法理論研究進展的推進，這些困難問題的安全性都會發生變化。如RSA加密算法，NIST密鑰管理準則認為，2010年后，1024位的密鑰不再安全，需要增加到2048位的密鑰長度，預計其安全有效性可以保持至2030年。

對于企業而言，這里的啟示在于，不能簡單地認為，隱私保護技術方案現在有效，就保證了10年后依舊有效。無論什么樣的隱私保護技術方案都有其時效性。

企業如果能夠根據權威技術組織推薦的安全參數、算法方案及時更新現有的系統，困難性理論就能夠有效保障隱私保護技術方案的有效性歷久如新。

正是：密碼學技術易守難攻，困難性理論當居首功！

作為密碼學安全的基石，計算困難問題和相關的安全參數，是企業有效進行密碼學算法選型的關鍵考察點。企業應用落地時，需充分考慮隱私數據保密的有效期，選擇合適的密碼學算法和密鑰長度，對數據安全性和系統效率進行必要衡量。

除了與密碼學算法直接相關的計算困難問題，一個完整的隱私保護技術方案通常還需要構造密碼學協議，來組合多種密碼學算法。密碼學協議引入了多方之間的交互，由此也引入其他重要的安全假設。

這些安全假設對評價隱私保護技術方案的整體安全性、有效性、實用性至關重要，具體分析，敬請關注下文分解。

Tags：區塊鏈比特幣HYPHYPE區塊鏈技術通俗講解簡書比特幣以太行情Masternode Hype Coin ExchangeHyperLending

中幣