LIC:云中「秘密」：構建非交互式零知識證明---探索零知識證明系列（五）

本文作者：郭宇

Onceexposed,asecretlosesallitspower.一旦泄露，秘密就失去了全部威力―

AnnAguirre

這已經是本系列的第五篇文章了，這一篇繼續深入非交互式零知識證明。本文約12,000字。

系列一：初識「零知識」與「證明」

系列二：理解「模擬」

系列三：尋找「知識」

系列四：隨機「挑戰」

提綱

CRS的前世今生

哈密爾頓環路問題

云中的秘密：HiddenBits

升級隨機性

FLS變換：從HiddenBits到NIZK

尋找理想的TrapdoorPermutation

NIZKProofvs.NIZKArgument

沒有秘密的世界

追到這里的讀者想必已對零知識證明有了一個大概的認識。你是否想過這個問題：零知識證明為何可行？這里請大家思考一下（比如

系列一中的地圖三染色問題的流程）……下面兩個要素

似乎必不可少：

「交互」：驗證者通過多次反復挑戰，把證明者作弊概率降低到一個極小的值

「隱藏隨機性」：驗證者產生讓證明者無法預測的隨機數進行挑戰

然而對于非交互式零知識證明——NIZK來說，如何實現上面兩點？在

系列四我們介紹了如何采用「隨機預言機」來扮演一個虛擬的「第三方」角色，實現虛擬的「交互」與「隨機挑戰」。本文將深入講述另一種方法，如何通過一段共享的字符串去除「交互」與「隱藏隨機性」。這個字符串必須事先由「第三方」來隨機產生，這就是傳說中的「公共參考串」。

CRS的前世今生

假如我們不借助任何其它手段，限定證明者Prover和驗證者Verifier只能進行「一次交互」來實現「零知識證明」，那么他們只能證明「平凡」問題，也就是計算復雜類BPP，而這個復雜度類大家一般猜想可能等價于P。

注：如果Prover與Verifier只做一次交互，在這樣的NIZK系統中，我們很容易能構造一個DecisionProcedure——Verify(x,Sim(x))，來證明和證偽定理，因此只能證明平凡問題BPP。

平凡問題雖然也可以零知識證明，但沒有意義！怎么理解呢？因為驗證者直接可以在多項式時間內根據「輸出」求解出「秘密輸入」，雖然驗證者能夠求解，但是「證明」本身并沒有額外為驗證者提供更多的「知識」。換句話說，不需要證明者出示證明，驗證者就知道命題為真，于是證明過程也是零知識的。

因此，當我們討論「零知識證明」時，要考慮帶「知識」的NP類問題。大家都知道，P問題是「確定性圖靈機」多項式時間內可以求解的復雜類，它的執行路徑對于輸入x是一個線性的狀態轉移。而NP問題是「不確定性圖靈機」多項式時間可以求解的問題類。所謂的不確定性圖靈機，就是它每次往前走一步是不確定的，有很多個選擇，只要任何一個執行路徑能到達終止狀態，就表示它解決了該問題x。換句話說，它的執行軌跡是一棵樹。那么如果我們把不確定性圖靈機每一步的路徑選擇記錄下來，那么把(x,witness)交給一個確定性圖靈機，那么它也能在多項式時間內解決掉x問題。

再強調一下，「知識」能提高圖靈機的解決問題的能力。

NP問題中存在著不想「泄露」給驗證者的知識witness，這時，在一個交互式證明系統中，證明者和驗證者在「知識」的掌握程度上是不對等的。

為了保證證明過程的「零知識」，我們需要保證：模擬器與驗證者的不對等。可是，模擬器沒有witness啊，怎么能讓他們不對等呢？上一篇我們介紹了「隨機預言機」，我們通過允許讓模擬器可以綁架「隨機預言精靈」的方式制造不平等。本篇將講述如何利用CRS來制造不平等。

CRS是一個在證明之前就已經公開的，并且在證明者與驗證者之間共享的，隨機字符串。我們怎么來使用CRS呢？直覺上，一串雙方都「知道」的信息，并不會增加「知識」不對等的情況。

首先大家會想，能不能直接用CRS作為隨機挑戰數呢？可不可以讓CRS來代替「隨機預言精靈」的角色？答案是不行！

為什么？這是因為CRS是在證明之前就已經產生了，如果證明者Prover提前知道了所有的隨機挑戰數，那么很顯然這個隨機挑戰也就失去了意義。

注：請大家回想下「隨機預言機」是如何保證證明者無法提前預測「隨機挑戰數」的？沒想明白的你，請重讀系列。

CRS的使命就是讓「模擬器」與「驗證者」不平等。怎么做呢？隱藏一些「秘密」進去。

如果進一步追問，隱藏了「秘密」有什么用呢？當然有用啦，在「理想世界」中，模擬器與抽取器才能很開心地玩耍起來……

1988年，ManuelBlum，PaulFeldman和SilvioMicali三位先驅發表的論文「Non-InteractiveZero-KnowledgeandItsApplications」展示了「交互」與「隱藏隨機性」的不必要性。他們給出了一個地圖三染色問題的NIZK證明系統，在一段共享的隨機產生的字符串的幫助下。

不過，……，我不會告訴你這個方案需要共享大概n^4超長的CRS，其中n是要證明的「命題」的長度。

1990年，UrielFeige，DrorLapidot與AdiShamir三人提出了另一種構造NP語言的NIZK方案。與不一樣的是，這個NIZK方案不再基于特定的數論假設，而是基于一個密碼學工具TrapdoorPermutation。在這個方案中，FLS提出了「隱藏比特」的概念，然后把HiddenBits藏入了CRS。對于模擬器而言，就可以通過修改CRS中的HiddenBits來達到模擬的效果，從而體現出對驗證者Verifier的優越性。不過，這個方案需要共享更長的CRS，超過k*n^5，這里k是安全參數。

此后，HiddenBits的思路被很多人采用，值得一提的是，Kilian與Petrank采用了一種更巧妙的方法來使用HiddenBits，成功地把CRS的長度縮減到了k*n^2。后來J.Groth繼續優化，把CRS的長度縮小到了大約k*n。

派盾：BSC上LW代幣遭遇攻擊，損失約5萬美元:5月12日消息，據派盾預警監測，BSC上LW代幣遭遇攻擊，損失為48,415 USDT，LW代幣價格暴跌69%。攻擊者已經將約150枚BNB轉移到Tornado Cash。[2023/5/12 14:58:56]

除了HiddenBits，J.Groth，R.Ostrovsky與A.Sahai使用了同態加密方案Boneh-Goh-Nissim或Boneh-Boyen-Shacham來實現NIZK，他們把加密方案的「公鑰」當做是CRS，同時Prover加密作為證明，然后利用同態性質來證明另一個NP-Complete問題——布爾電路的可滿足性問題。這個方案的最大優點，就是CRS長度是固定的，因為只是一個密鑰而已，長度只有k。對于模擬器而言，它可以通過超能力，拿到這個公鑰所對應的陷門，從而能夠實現密封任何信息，但得到相同的密文；對于抽取器而言，它可以用超能力拿到公鑰對應的私鑰，從而能夠解密證明得到「知識」。

JensGroth在2010年基于KEA假設與Pairing提出了一種新的NIZKArguments方案，這也是后續許許多多zkSNARKs方案的起點。這里的CRS由一對對的構成，被用來實現「知識承諾」。其中x與?是兩個隨機數，在產生完CRS之后，必須被「遺忘」。有些人把這部分需要遺忘的隨機數叫做「ToxicWastes」，這容易誤導讀者。他們不僅無無害，而且非常有用。他們是被藏入CRS的「秘密」，是模擬器的武器。如果模擬器得到了x與?，就能偽造證明，從而保證證明的零知識。而對于抽取器，他能直接通過KEA假設內建的抽取函數來抽取知識。

最新的Sonic方案又在的基礎上實現了UpdateableCRS。如果任何人擔心CRS中的秘密已經被泄露了，他就可以在原有CRS基礎上打一個補丁，繼續往里藏一個秘密，這樣就能保證CRS的安全性。這里的CRS還是「Universal全局」的，即CRS只需要生成一次，就可以應付所有的命題證明。這個方案后續被最新的Plonk，Marlin等方案采用。

接下來，我們就從一個簡單的例子開始，理解如何基于CRS來構造NIZK。在這之前，我們需要介紹一個NP-Complete問題——哈密爾頓環路問題。

哈密爾頓環路問題

想象出一個地圖中有若干個城市，城市與城市間可以有公路。

假如給你一副地圖，讓你找出一條路徑，不重復地走遍所有的公路。相信你會馬上興奮起來，這不就是小時候學過的「一筆畫」么？判斷一個地圖能否一筆畫，這是小學生做的數學題，我們可以計算每個城市連接的公路個數，根據奇偶性分成「奇點」與「偶點」。如果一個地圖中存在兩個奇點城市，那么你只能從一個奇點城市出發，遍歷所有的公路，并且最終到達另一個奇點城市。這條路徑就被稱為「歐拉路徑」。

如果一個地圖中所有的城市都是偶點，那么你可以從任意一個城市出發，輕松地找出一條路徑，不重復地遍歷所有的公路，并且回到起點。這個環路被稱為「歐拉環路」。

而如果地圖存在超過2個以上的奇點，那么就不存在歐拉回路，比如著名的哥德斯堡七橋問題。

著名的哥德斯堡七橋問題就是這么描述，如果不重復地穿過下面七座橋。

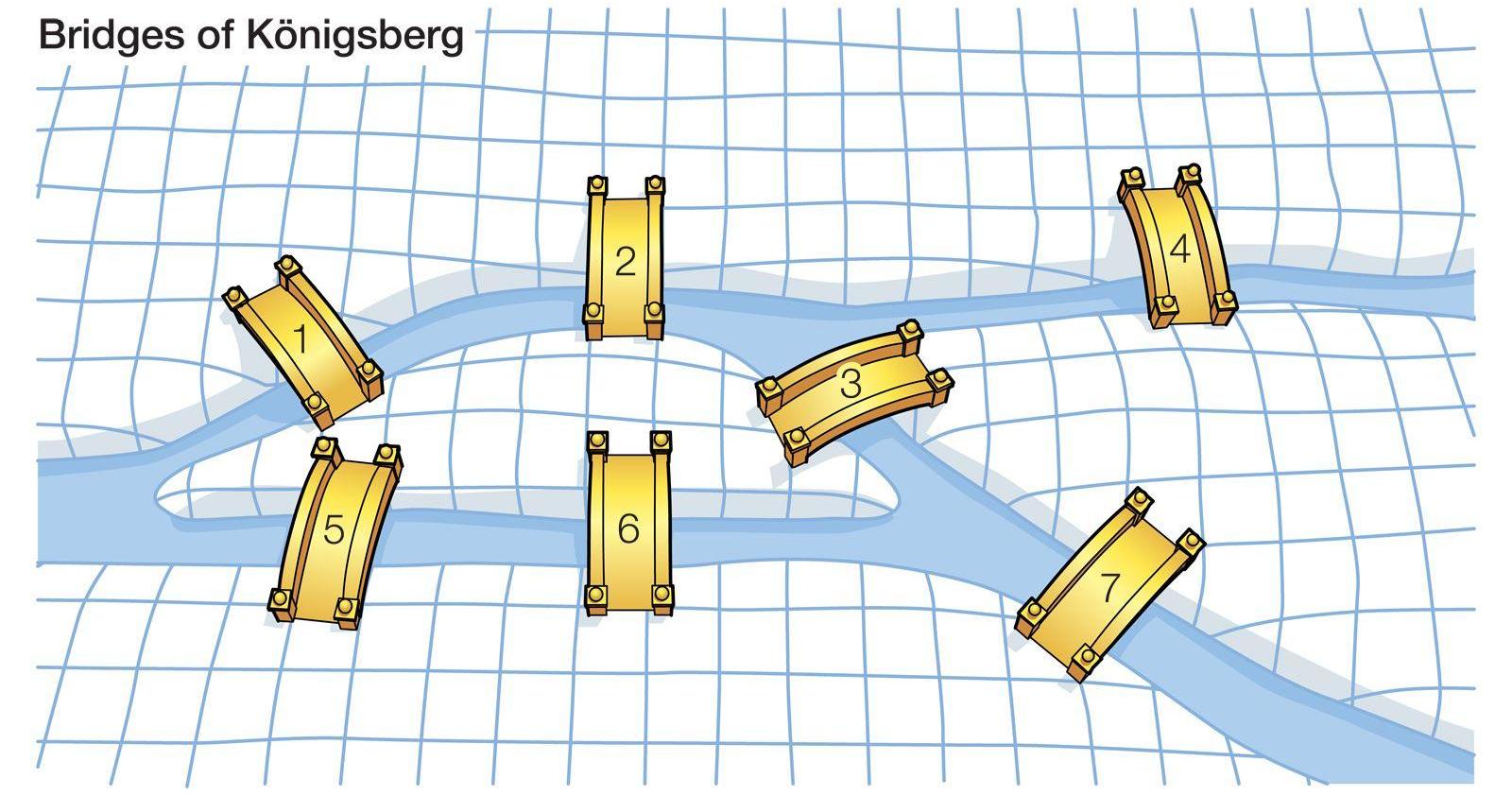
哥德斯堡七橋地圖顯然存在多個奇點，不存在歐拉路徑。如果給定任何一個地圖，是否存在一個歐拉環路，這是一個P問題，也就是一個計算機可以在poly(n)多項式時間內尋找。

注：歐拉環路的尋找算法被稱為Fleury算法。

對于這樣一個P問題，如果一個證明者Prover證明他知道一個歐拉回路，那么他可以直接發送回路的明文，然后驗證者Verifier驗證回路正確與否。請注意，這個過程仍然是零知識的。因為，Verifier并沒有通過Prover發送的信息獲得任何額外的知識。換句話說，Verifier并沒有因為看到回路，而增強了自身計算能力，因為Verifier本來就可以自行計算歐拉回路。

而我們要講的是「哈密爾頓環路問題」則是一個NP問題，描述如下：

是否一個地圖存在一個環路，能不重復地穿過每一個城市。

比如下面這張地圖：

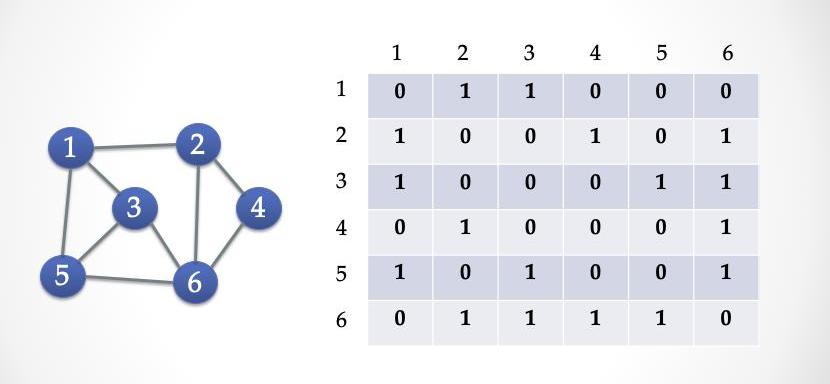
我們用一個矩陣V*V的矩陣來表示這個地圖，凡是兩個城市有公路相連接，那么就在(A,B)和(B,A)里面填上1，否則填0。這個矩陣被稱為「鄰接矩陣」，我們可以把這個鄰接矩陣拍扁，就變成了一個0/1比特串。

尋找「哈密爾頓環路」是一個NP-Complete問題，換句話說，不存在一個算法使得計算機在poly(n)多項式時間內找到環路。但是，計算機可以在多項式時間內檢驗一個路徑是否是「哈密爾頓環路」。比如這個地圖中就有一個帶方向的哈密爾頓環路，我們一眼就能驗證這個環路確實穿過了每一個城市。如果一個地圖有哈密爾頓環路，那么它的矩陣一定是滿足下面的特征：每一行一定有一個1，每一列一定也有一個1。

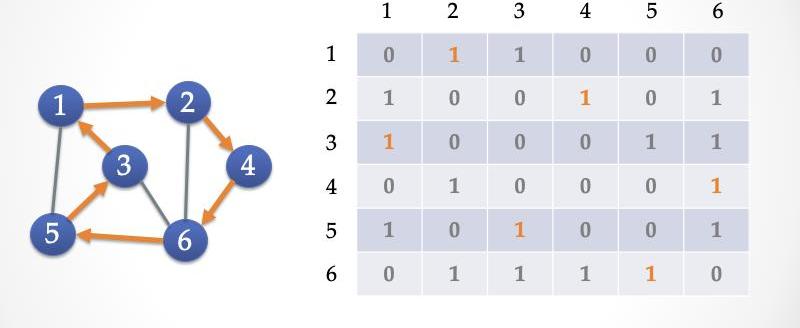
ZK-HAM協議

我們下面給出一個三步交互的Sigma協議，Alice向Bob證明她「知道」上面這個地圖G的哈密爾頓環路。

公共輸入：G為一個有6個頂點的地圖，表示為一個6*6的鄰接矩陣

秘密輸入：G的哈密爾頓環路C

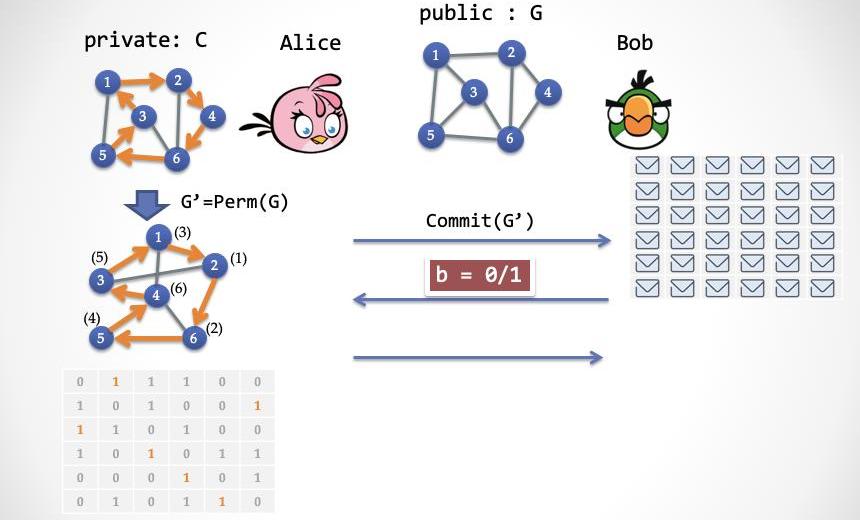
第一步：Alice隨機選擇一個「置換」，Perm(.)，然后通過這個置換，產生一個新的圖G'；然后Alice把G'矩陣的每一個單元加密，產生一個新的矩陣發送給Bob。

今日恐慌與貪婪指數為46，恐慌程度顯著下降:1月14日消息，今日恐慌與貪婪指數為46（昨日為31），恐慌程度較昨日大幅下降，等級仍為恐慌。

注：恐慌指數閾值為0-100，包含指標：波動性（25%）＋市場交易量（25%）＋社交媒體熱度（15%）＋市場調查（15%）＋比特幣在整個市場中的比例（10%）＋谷歌熱詞分析（10%）。[2023/1/14 11:11:30]

：所謂置換，大家可以想象成用

鼠標隨意拖動圖中的點，但是點和點之間的連線會跟著點一起被拖動，拖動結束之后形成的圖，進行重新編號就得到G'，比如上圖左側的兩個圖。經過置換變換的圖前后是

同構的。其中下圖中，每一個頂點上角括號中的標號為拖動之前該頂點在上圖中的編號。形式化一點可以這么定義：Perm()是一個{1,V}到{1,V}的雙射函數新圖G'的鄰接矩陣，=1當且僅當=1，其中i是頂點編號，V是頂點個數。

第二步：Bob隨機選擇bin{0,1}}進行挑戰。

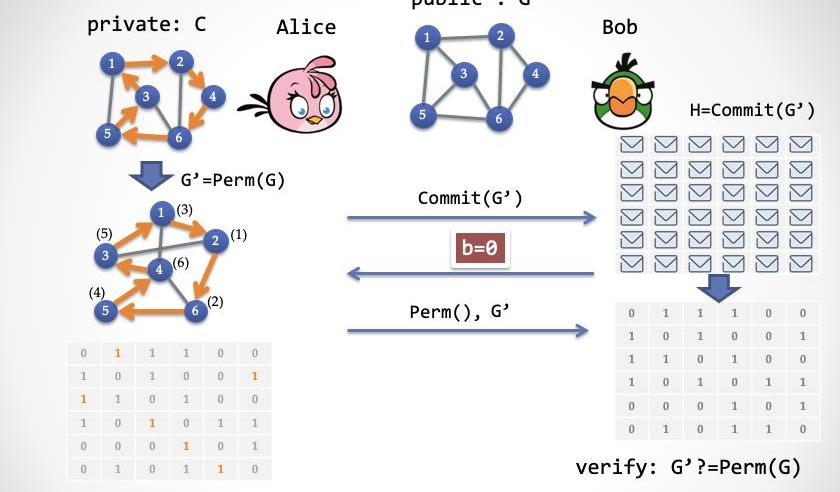
第三步情況：Alice根據Bob第二步發送的值：如果b=0，那么Alice發送置換函數Perm()，并且揭示完整的圖G'。而Bob則確認G'是否是原圖G經過置換無誤。

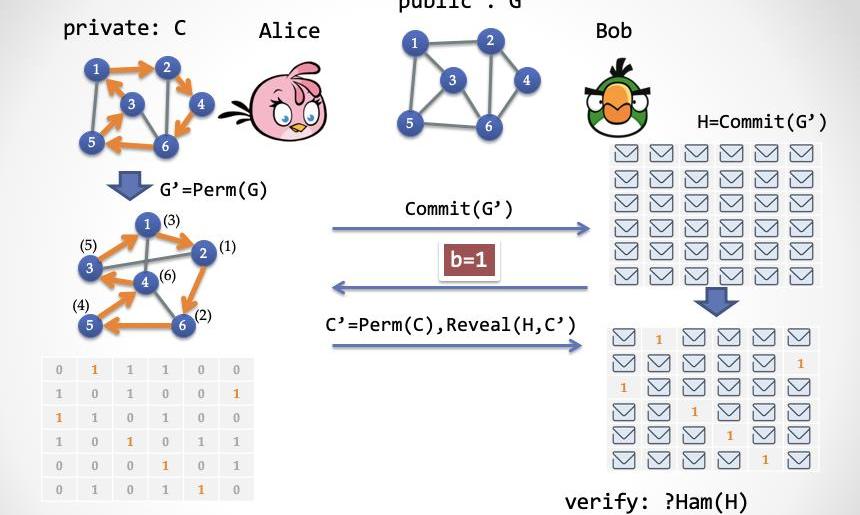
第三步情況：如果Bob第二步發送的b=1，那么Alice只揭示G'中的哈密爾頓環路C'即可。而Bob需要驗證C'是否是一個哈密爾頓環路

回憶一下三步Sigma協議，我們再理解下上面看似復雜的動作：

第一步：被稱為Commit，證明者Alice需要把手里的答案進行同態變換，產生一個新答案，然后把每一條邊都鎖起來，交給Bob；

第二步：Bob進行隨機挑戰；

第三步：Alice根據Bob的隨機挑戰，做出兩種不同的回應。如果Bob挑戰0，那么Alice打開第一步的承諾，表示自己在第一步沒有作弊；如果Bob挑戰1，那么Alice只解密暴露出哈密爾頓環路的邊，其它邊則不需解密。Bob可以輕易地檢查地圖上露出來的那些邊是否構成了一個不重復地經過所有城市的環路。

如果這個Sigma協議只走一遍的話，Alice作弊的概率是50%，如果重復n遍，Alice作弊概率會指數級減小。大家可以試著用「模擬器」和「抽取器」的方法來證明這個協議的「零知識」與「可靠性」。

ZK-HAM的變形：ZK-HAM-2

接下來把上面的這個三步協議改動一下。大家先考慮下這樣一個簡單事實：如果一個僅包含環路的子圖C是圖G的子圖，C<=G那么說明G包含哈密爾頓環路。

這個事實等價于另一個事實：一個哈密爾頓圖G的補集!G是環路子圖C的補集!C的子圖。

圖的補集：所謂補集就是這樣一個新地圖，頂點保持不變，舊地圖上的邊在新地圖中不存在，而新地圖中的公路在舊地圖中不存在，但是兩個圖重合在一起，就變成了一個完全圖。

用鄰接矩陣來理解，就是如果一個圖G包含一個環路子圖C，那么G矩陣中所有值為0的單元集合必然被C矩陣中所有值為0的單元集合包含。可以表示為!G<=!C。

根據第二個事實，我們可以定義如下的Sigma協議：

公共輸入：圖G，表示為6*6的鄰接矩陣

秘密輸入：G的哈密爾頓環路C

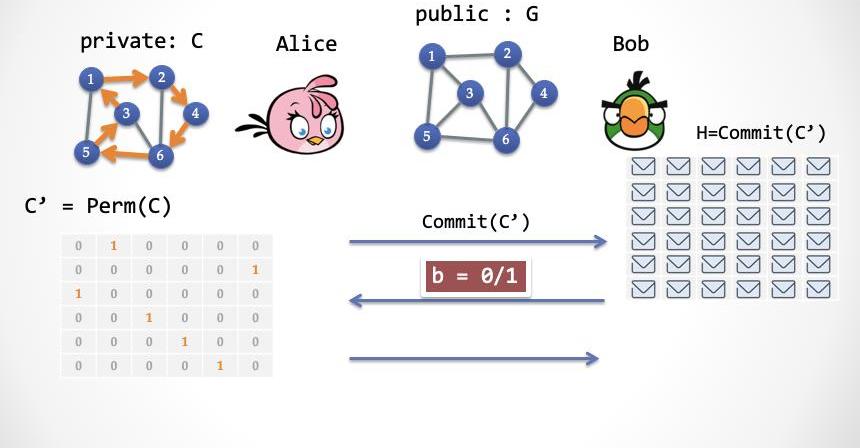
第一步：

Alice隨機選擇一個「置換」，Perm(.)，并且通過C構造一個哈密爾頓環路子圖C'=Perm(C)；

然后Alice加密C'的每一個單元，把解密后的結果發送給Bob。

第二步：Bob隨機選擇bin{0,1}進行挑戰

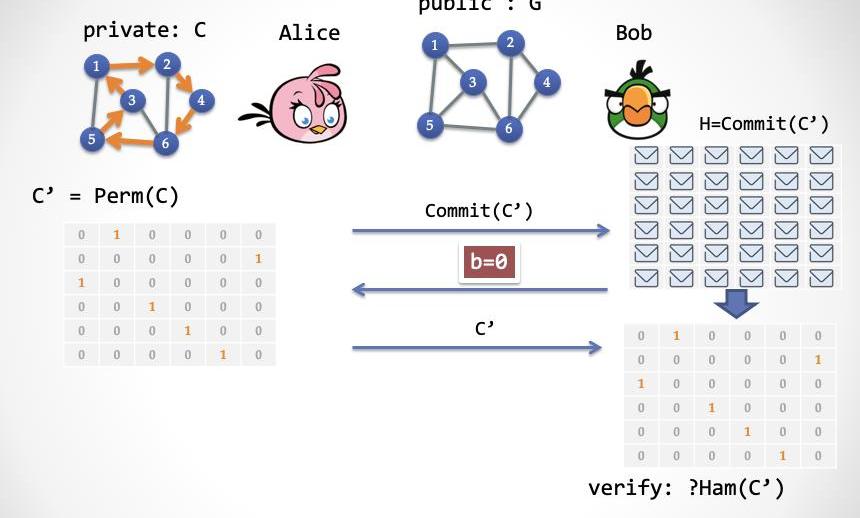
第三步情況：如果b=0，Alice揭示完整的C'，而Bob驗證這個C'是否確實是一個哈密爾頓環路子圖。

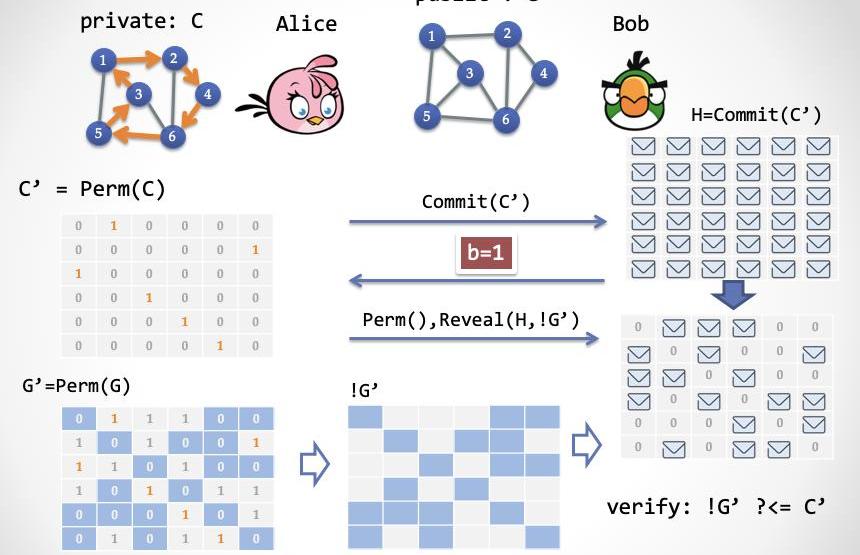
第三步情況：如果b=1，Alice發送Perm()，同時按照G'=Perm(G)中的所有含0單元所在的位置，揭示C'中所對應的單元；Bob驗證C'所有被揭示單元是否全部為0。

再理解下這三步Sigma協議：

第一步：證明者Alice需要把哈密爾頓子圖C進行置換變換，產生一個新的哈密爾頓子圖C'，加密后交給Bob；

第二步：Bob進行隨機挑戰，0或者1；

第三步：如果Bob挑戰0，那么Alice打開第一步的承諾，展示一個帶有唯一環路的圖；如果Bob挑戰1，Alice則按照G'中的0單元的位置打開承諾，展示承諾中被打開的位置全部為0。

重點來了，大家仔細看看這個新版的Sigma協議的第一步。有沒有發現什么情況？

第一步Alice發送的內容是與地圖G無關的！

同樣，第二步Bob發送的挑戰也是與地圖無關的。這樣我們可以把第一步發的承諾改成事先準備好的比特串，而且我們假設這個比特串由一個可信第三方來產生，這樣一來Bob就沒有必要發送b=0這個分支，因為可信的第三方是誠實的，他一定是事先準備好一個正確的環路子圖。這樣，由于Bob只需要發送1挑戰分支，那么這一步也可以去除。

于是，三步協議變成了一步，我們成功去除了交互，有望實現NIZK。

我們接下來把ZK-HAM-2協議的第一步和第二步推到一個事先準備的字符串中，然后只讓Alice發送第三步的內容給Bob。如下圖所示：

美國銀行：加密貨幣繼續充當風險資產:金色財經報道，美國銀行（BAC）周五在一份研究報告中稱，數字資產繼續充當風險資產，隨著全球利率上升而下降。盡管如此，最終復蘇的積極跡象包括穩定幣的流入。上周這些流入量躍升至 4.9 億美元，比前一周高出 58%，四大穩定幣連續第三周出現外匯凈流入，并指出幣安美元（BUSD）大量流入/美元硬幣（USDC）流出可能是投資者“搶先從USDC轉向”BUSD的結果，避免在幣安決定將一些穩定幣自動轉換為自己的穩定幣后造成干擾。

此外，美國銀行希望監管的明確性能夠支持DeFi的采用。[2022/9/26 22:30:02]

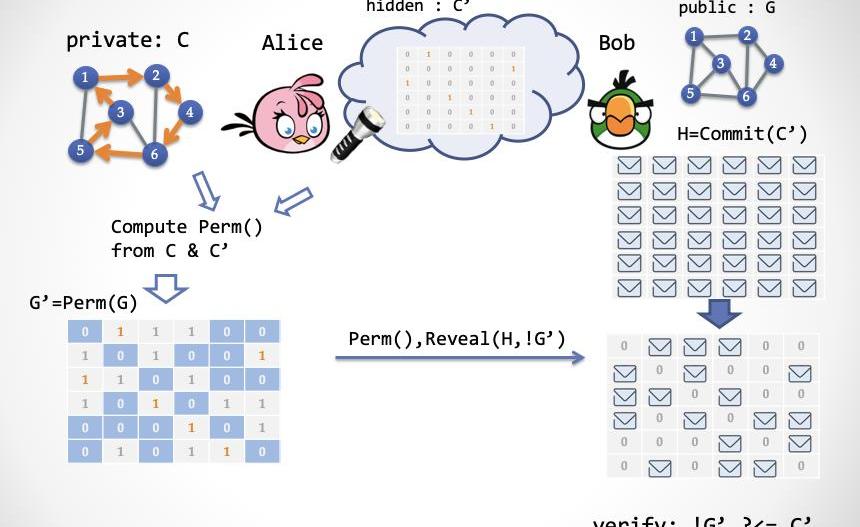
請注意，這里還不算是一個NIZK系統，因為這個共享字符串并不能對Bob公開，否則Bob就能算出環路C。接下來，我們要解釋一個新概念：「隱藏比特」。HiddenBits是這樣一串隨機比特，它們對于驗證者Bob隱藏，但是對于證明者Alice公開。然后在證明過程中，Alice可以選擇性地揭示一部分比特展示給Bob看。這是構造NIZK證明系統的一個利器，下面我們需要再繼續深入……

云中的秘密：HiddenBits

讓我們再次開下腦洞，想象天上有朵云，云后面藏著一串隨機產生的比特值，不是0就是1，然后Alice帶著一個「超級眼鏡」，于是能夠看到云后面所有的隨機比特串，但是Bob卻看不到。同時Alice手里還有一個「超級手電筒」，她可以打開手電筒用激光穿透云層，讓Bob也能看見其中某個或某些比特。當然，Bob能看到的比特的選擇權完全在Alice手中。

云朵中隱藏的比特串就是所謂的HiddenBits。

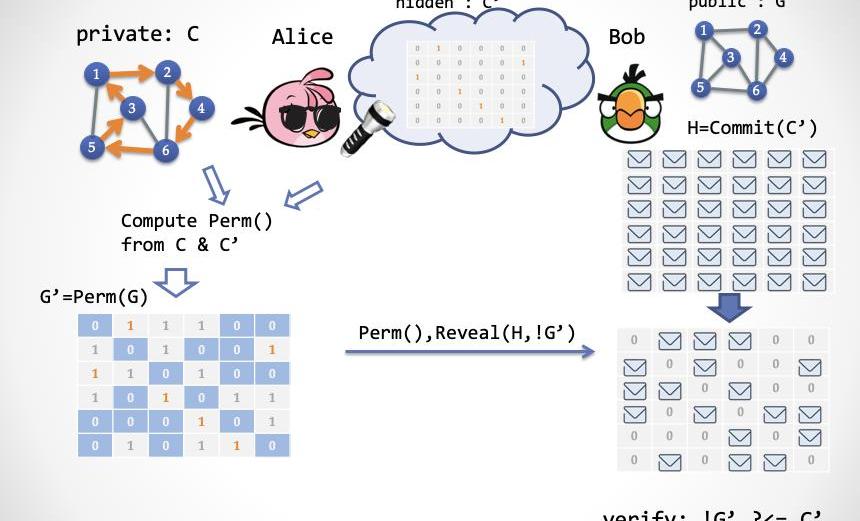
接下來我們要通過HiddenBits來完成一個單步交互，完成ZK-HAM-2協議的功能。在ZK-HAM-2中的第一步，Alice產生一個隨機的置換Perm()，然后通過G中的哈密爾頓環路子圖C產生一個變換后的環路子圖C'=Perm(C)。這等價于，事先由任何人產生一個隨機的哈密爾頓環路子圖C'，然后Alice根據C和C'計算得出一個相應的Perm()。

假設由某個「第三方」產生了一個隨機的環路子圖C'，編碼成「鄰接矩陣」比特串，放到云朵后面。假設V為頂點的個數，E為邊的條數。這個鄰接矩陣的編碼需要一個V*V長度的比特串，可以解釋成一個V*V的矩陣，其中每一行只包含一個1，每一列也只包含一個1，矩陣的其它單元都為0。

接下來Alice如何構造證明呢？這其實很簡單：

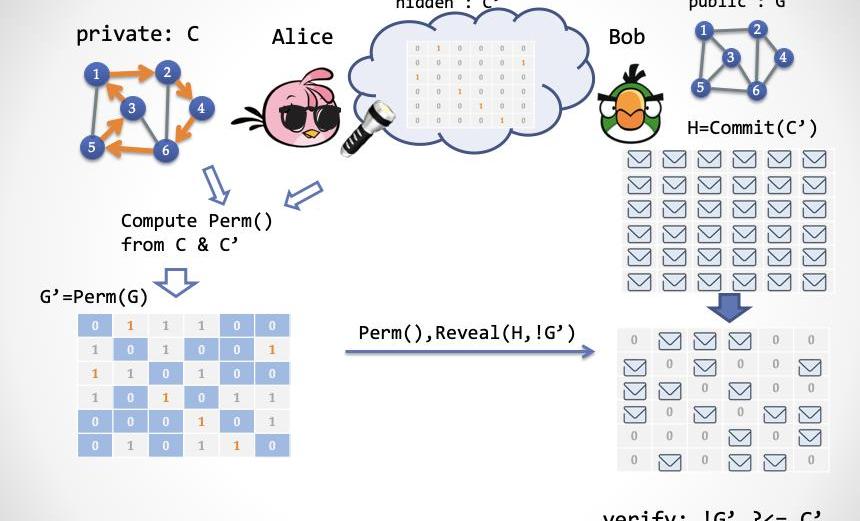
Alice通過「超級眼鏡」得到了一個隨機的哈密爾頓環路子圖C'，然后計算得到一個置換Perm()，使得Perm(C)=C'。

Alice根據Perm()來計算出一個換后的圖G'=Perm(G)

Alice產生證明，由兩部分組成：置換Perm()G'的鄰接矩陣中所有值為0的單元坐標所對應的C'矩陣的值，相當于Alice需要用「超級手電筒」給Bob揭示的隱藏比特。

那么Bob怎么驗證這個證明呢？Bob拿到證明之后，只需要檢驗兩個東西：

Perm()是否是一個合法的置換V->V，比如不能出現兩個頂點映射到同一個頂點的情況。

對于G中的每一條「非邊」，經過置換之后，Bob抬頭看天上對應的「隱藏比特」，比特值必須為0

我們再仔細地深入理解下這個非交互協議。先從「完備性」入手：如果Alice沒有作弊，那么很顯然能夠通過Bob的驗證，這里請大家自行檢查。

接下來我們分兩步簡要證明下「可靠性」：首先，因為Bob經過驗證得知，所有G置換后的非邊集合都已被揭示，且全為0，那么可以得出結論，!G<=!C，即G的非邊集合是環路子圖C的非邊集合的子集。這等價于，C<=G，也就是說G包含一個哈密爾頓環路。這里請注意，這個可靠性概率是100%。

然后，設想在一個「理想世界」中，Bob獲得了某種超能力，不需要Alice的超級手電筒，就能看穿云層，得到所有的隱藏比特C'。然后當Bob得到Perm()之后，就能通過Perm()反算出C，于是Bob就相當于變身成了一個「抽取器」，在理想世界中，它能把Alice要證明的知識給成功抽取出來。

那么怎么證明「零知識」呢？Alice要具備一個超能力，就是在「理想世界」中，可以偷偷修改云朵中的隱藏比特。接下來就簡單了，模擬器Zlice可以這么欺騙Bob：

Zlice把云朵中的隱藏比特全部置為0

Zlice隨機產生一個合法的Perm()

大家發現了，關鍵是，天上隱藏的比特必須是一個可信的字符串，所謂「可信」，就是指它確實應該是一個哈密爾頓環路子圖。那么第三方需要可信。

可是，這樣一個第三方是不是難以令人滿意？Alice和Bob要絕對信任他，不會和對手串謀。如果他和Alice串謀，可以把隱藏比特串直接設置為全0；或者他和Bob串謀，直接把這個比特串給Bob看。這個協議看起來不錯，但是很難實用。我們接下來要對這個簡單協議進行升級。

升級隨機性

第一個升級是讓隱藏比特串變成一個「一致性均勻分布」的隨機的隱藏比特串，是一個看起來相當隨機的比特串，而不是一個刻意擺放好的哈密爾頓子圖。

完全隨機意味著比特串中的0的個數和1出現的概率大概接近。那么接下來一個難題是如何讓隨機比特串中能出現一個隨機的哈密爾頓環路子圖矩陣。方法非常簡單粗暴：產生一個足夠長的隨機串，然后從頭掃描，直到找到一個隨機的哈密爾頓環路為止。

可是……這個成功概率是不是非常非常小？我們下面給出一個概率沒那么小的一種尋找方法。

Kava 11將于北京時間10月13日發布:9月14日消息，據Kava Network官推消息，Kava 11將于UTC時間10月12日17:00（北京時間13日凌晨1點）正式發布。[2022/9/14 13:29:43]

我們先把比特串按照5log(V)的長度進行切分，然后如果每一個分片中的所有比特全為1，那么我們把這個片段被視為鄰接矩陣中的一個值為1的單元，否則視為一個值為0的單元。這樣每一個矩陣單元出現1的概率為1/(V^5)。

我們取連續的V^6個片段，構成一個V^3*V^3的大矩陣。如果大矩陣中包含一個V*V的哈密爾頓環路矩陣，并且其他單元都為0。那么我們稱這個大矩陣為「有用」。

根據概率計算，出現一個「有用」矩陣的概率為1/。

注：「有用」矩陣的概率計算過程請參考Fact4.10.8,「FoundationsofCryptography,VolI」byOdedGoldreich，P304。

好了，我們需要升級下上一節的協議。因為現在「隱藏比特串」被拆分成了若干個大矩陣，這些大矩陣有些是「有用」的，有些是沒用的。

接下來Alice要來構造證明了，她先戴上超級眼鏡，掃描云朵中的HiddenBits，這要分兩種情況，

Case1：如果Alice遇到了一個沒用的大矩陣M，Alice公開M的所有單元。

Case2：如果Alice遇到了一個「有用」的大矩陣M，這意味著Alice得到了一個隨機的哈密爾頓環路C'，然后Alice參照上一節的步驟進行證明即可。

那么Bob怎么驗證這個證明呢？我們還要分情況進行討論，

Case1：如果Alice公開了全部的M，那么Bob就檢查這個M是否「無用」。如果M無用，就認為證明有效；否則拒絕。

Case2：如果Alice發送的是形如這樣的證明，那么Bob按照上一節的驗證方法進行驗證。

對于這個協議，Bob已經不再擔心第三方是否作弊，故意產生一個全零的比特串，但是Alice仍然擔心一旦第三方和Bob串謀，那么知識就徹底泄露了。

不僅如此，現在的協議還有個很強的限制，Alice不能在看到隱藏比特之后再選擇需要證明的G，否則Alice就可以作弊。如果一個證明者選擇證明的「命題」與CRS無關，那么這個證明者被稱為Non-adaptiveAdversary。

FLS變換：從HiddenBits到NIZK

接下來，我們再次升級協議，把「隱藏比特串」中的隱藏特性去除，變成「公共參考串」CRS。這里我們要借助一個密碼學工具——TrapdoorPermutation，陷門置換。

所謂的陷門置換是指一個置換函數F(x)，x是一個集合S中的元素，然后函數F(x)把x映射到S中的另一個元素y。同時F(x)滿足單向性，即通過y很難反算出x；但是如果誰擁有陷門t，就能實現反向計算F^(-1)(t,y)=x。陷門置換還可以匹配一個HardcorePredicate，h(x)=0/1，它能根據S集合中的元素產生一個一致性分布的0/1比特。介紹完畢，大家是不是有點暈，沒關系，暈一暈就習慣了。總之一句話，陷門置換可以對公共參考串和HiddenBits進行相互轉換。

先假設有這樣的密碼學工具，然后我們升級協議。

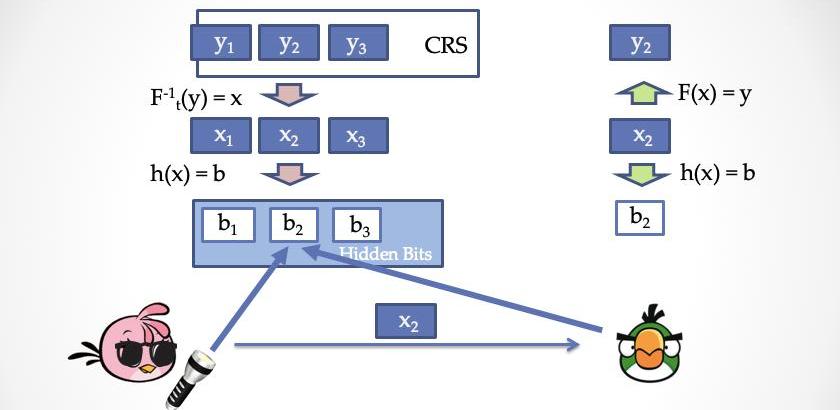
我們把公共參考串看成是一個列表，y1,y2,y3,...,yn，列表中的每一項都是集合S中的元素。然后通過HardcorePredicate產生HiddenBits中的每一個比特位。但是請注意，這里不能直接通過h(y)=b來產生HiddenBits，因為這樣一來Bob就能自己算出所有的HiddenBits，這違反了上一節的協議。為了保證對Bob隱藏，我們需要用公共參考串的原象，也就是x1,x2,x3,...,xn來產生HiddenBits，h(x)=b。Bob雖然不能自己計算b1,b2,b3,...,bn，但是一旦得到一個x，他就能檢驗F(x)?=y來判斷是否x是和公共參考串對應，同時再計算h(x)=b得到被揭示的HiddenBits，b。

我們可以換一種不太準確，但是更直觀的方式來理解，Alice相當于自己產生一對公私鑰。然后Alice把公共參考串看成是一段「密文」，由于Alice有私鑰，于是可以對密文進行解密，得到明文，這些明文，對于Bob而言就相當于是HiddenBits。當Alice要「揭示」HiddenBits時，就出示相應的明文片段，并且帶上公鑰，那么Bob就能通過公鑰再次「加密」明文，與公共參考串的密文進行比對，確保Alice沒有在揭示過程作弊。

下面是升級后的協議：

對于證明者Alice：

Alice隨機選擇一個TrapdoorPermutation，(F,h,t)

根據公共參考串中的每一個yi，利用陷門反向計算出xi=F^(-1)(t,yi)

計算HiddenBits，bi=h(xi)

根據上一節的協議產生證明。假設Alice要揭示的Hiddenbits的位置集合為r1,r2,...,rl，那么Alice向Bob發送對應位置的x，分別為x_r1,x_r2,x_r3,...x_rl，連同(F,h)，和證明一起并發給Bob。

對于驗證者Bob：

檢查(F,h)是否為一個合法的TrapdoorPermutation。

對L中的每一個元素x_r，計算出被揭示的HiddenBitsbi=h(F(x_r))，然后按照上一節的協議檢查證明。

這個新協議的「完備性」，請大家自行檢查。

對于「零知識」，我們需要構造一個「模擬器」Zlice2，它的超能力是修改公共參考串。

模擬器直接調用上一節協議的模擬器Zlice。得到一個三元組，(proof,{r},{b})

Celo成立Celo Web3非洲基金，助力非洲初創公司采用加密策略:7月12日消息，Celo宣布成立Celo Web3非洲基金，以幫助成功的非洲初創公司采用加密策略，目前正在接受創始人申請。[2022/7/12 2:07:30]

對于每一個公共參考串位置，如果它對應某一個r，模擬器從集合S中隨機選擇一個x_r，使得h(x_r)=b_r，這里b_r就是{b}中對應r；然后把y_r=F(x_r)作為假參考串的一部分。

對于每一個公共參考串位置，如果與{r}無關，那么模擬器隨機選一個y即可

模擬器把所有的y拼在一起，得到一個假CRS。

對于「可靠性」，事情變得不那么簡單了。因為現在Alice有能力挑選(F,h,t)，Alice可以挑選一個對自己有利，甚至作弊的(F,h,t)，使得她可以控制一次協議運行的HiddenBits{b}的結果。對于本節升級后的新協議而言，需要重復很多遍，以致于雖然Alice可以控制一次協議運行的HiddenBits，但是她對其它若干次協議運行的HiddenBits無能為力。換句話說，Alice無論如何挑選(F,h,t)都無法完全掌控多次的協議運行。

這個升級變換理論上可以支持任意的HiddenBits模型下的非交互式零知識證明，被稱為FLSProtocol。FLS變換有很多的好處：首先，這個隨機產生的CRS可以多次使用，實現所謂的「Multi-TheoremNIZK」；其次，可以實現「AdaptiveSoundness」，即Alice可以先看到CRS，然后再選擇要證明的內容。最后，這個協議還是「AdaptiveZero-Knowledge」，即Bob也可以先看到CRS，然后再選擇要證明的內容給Alice。

注：AdaptiveAdversary是比較符合現實世界的安全情況，比如第二類CCA安全。因為CRS是公開的，攻擊者可以先分析CRS，再決定如何發起攻擊。

尋找理想的TrapdoorPermutation

陷門置換TrapdoorPermutation最早出現在姚期智老師的論文「TheoryandApplicationofTrapdoorFunctions」中，是公鑰密碼學的重要基礎。在上一節給出的FLS變換中，需要一個理想化的TrapdoorPermutation，所謂的理想化是指，每一個n-bit字符串都能唯一變成另一個n-bit字符串，并且不會出現「多對一」的映射關系。Alice需要隨機抽樣一個Index，發給Bob，然后Bob要能檢查出這個Index所對應的F()是否是一個「完美」的置換。問題來了，怎么Bob怎么能在多項式時間內檢查出來呢？如果Bob不能檢查，那么Alice就可以抽樣一個不完美的Permutation，從而可能作弊，破壞「Soundness」這個性質，Bellare和Yung發表在1996年的論文最早注意到了這一點，但是并沒有完全解決這個問題。

如何找到一個橋梁，能夠將TrapdoorPermutation合適地抽象出來，同時能夠對接到密碼學工具的實現上，是一個及其有挑戰性的工作。隨后各路密碼學家在這方面研究了很長時間，發表了許許多多的論文，各種不同類型的TrapdoorPermutation被定義、被研究，但是仍然不能讓人滿意。直到最近一個工作是RanCanetti與AmitLichtenberg提出了CertifiableInjectiveTrapdoorFunction這樣一個新類型，并證明了這種TrapdoorPermutation終于能滿足FLS變換要求。但這是不是故事的結束呢？理論密碼學家們估計不會停下探索的腳步。

除了基于TrapdoorPermutation的FLS變換，還有各式各樣的解決方案來升級HiddenBitsModel，比如采用InvariantSignature，或VerifiableRandomGenerator來實現HiddenBits的變換，或者弱可驗證隨機函數，還有一種叫做publicly-verifiabletrapdoorpredicates的方案。

三十年來，密碼學家們發明的NIZK方案有很多，但HiddenBits方法是目前已知唯一的辦法，(1)基于「一致性分布」的共享CRS，(2)實現任意NP語言的NIZKProofs。

NIZKProofs與NIZKArguments

在本文中，我們構造的NIZK「證明」系統的可靠性屬于「StatisticalSoundness」，而零知識則屬于「ComputationalZero-Knowledge」。這意味著什么呢？這意味著，不管證明者Alice的算力有多強大，Alice仍然無法作弊。但是，如果驗證者Bob擁有超強的計算能力，那么是存在這種可能性：Bob從證明中抽取到有價值的「知識」。

這又意味著什么？

這意味著，對于NIZKProofs來說，它的長度肯定要比「知識」長，知識即NP問題中的witness。只要Bob算力夠強，他就可以把證明解密。對于「抽取器」而言，它也需要在沒有交互的情況下抽取witness。證明最短的NIZKProofs當屬GregGentry等人采用「全同態加密」技術構造的NIZK方案了，證明長度只是稍稍大于witness的長度。

那能不能構造證明尺寸小于witness的NIZK呢？答案是YES！

還有一類的NIZK系統被稱為NIZKArguments：它們的可靠性是「ComputationalSoundness」，零知識屬于「PerfectZero-Knowledge」或者「StatisticalZero-Knowledge」。這說明，Alice如果算力超強，那么她是有作弊空間的，但是因為現實世界中，我們可以通過加大安全參數來極大地降低Alice作弊的可能性，但是能實現非常極致的零知識特性。由于弱化了可靠性，那么我們就可以繼續壓縮證明的尺寸。

注：在本系列中，我們并不刻意區分「證明」與「論證」這兩個詞。如果需要指明Arguments而非Proofs，會專門強調。

假如說我們要公開一個NIZK證明到Github上，假如過了一百年以后，Github網站還在，而未來計算機的計算能力已經有了質的飛躍，這時候，一個NIZKProof可能會被算力攻破，泄露知識，而NIZKArgument則很大可能性上還保持安全性。

現在流行的熱詞——zkSNARK中的AR正是指代Argument。

NIZKArgument可以實現O(1)常數級長度的證明，即與witness的長度無關。然而這需要隱藏更多的秘密到CRS中。

沒有秘密的世界

1956年，哥德爾在一封寄給馮諾依曼的信中提到了一個著名的問題，「P是否等于NP」。后來，這個問題被Clay研究所列為七個千禧年難題之一，懸賞百萬美金。

零知識證明系統正是為了保護witness不泄露的前提下，實現NP問題的驗證。那如果一旦證明了「P==NP」，這會意味著什么？這意味著witness不再有多大意義了，反正一個圖靈機也可以在多項式時間內找到witness。零知識證明試圖保護的witness也變得徒勞無益。

事實上，如果「P==NP」，現有的公鑰密碼學、對稱加密AES與SM4、哈希算法所依賴的難解問題都可能坍塌，我們可能很難保存秘密。不僅如此，

如果P==NP，我們所處的世界將會變得非常不一樣。「CreativeLeaps」將不再有價值，求解問題與驗證問題之間的鴻溝不復存在。每個能欣賞交響樂的人都會成為莫扎特，每個會推理的人都會變成高斯，每個能判斷投資好壞的人都會變成巴菲特。從達爾文進化論的觀點出發：如果這就是我們存在的宇宙，為什么我們還沒有進化得可以充分利用這個好處？——ScottAaronson(2006)

對于數學也一樣，數學證明的驗證過程也是多項式復雜度的，如果「P==NP」，那么也就存在著多項式時間尋找證明的算法。這意味著哥德巴赫猜想、黎曼猜想將有可能得到證明，難怪LanceFortnow在博客里這么說：

ApersonwhoprovesP==NPwouldwalkhomefromtheClayInstitutenotwithonemillion-dollarcheckbutwithseven.如果誰能證明P=NP，那么他不會只拿著一張百萬美元支票回家，而是七張。——LanceFortnow(2004)

2002年的調查顯示，61%的計算機科學家相信「P!=NP」，而十年后，這個比例上升到了83%。而我是被ScottAaronson的如下論斷說服的：

自指論證：如果P=NP是事實，那么這個證明會比較容易被發現；但是如果P!=NP，那么這個證明會比較難發現。所以相信P!=NP看起來會讓數學現實更一致一些。——ScottAaronson(2006)

盡管是如此不情愿，如果我們真的生活在一個沒有秘密的世界，那會是什么樣子？「環形監獄Panopticon」是18世紀英國哲學家JeremyBentham提出的一個驚悚概念。囚徒們被中心全天候監控，沒有任何隱私可言，而且他們對自己是否處于被監控狀態也無從得知。這個無比悲觀的論調讓人渾身不適，但很多人認為，這可能是兩百多年前對未來網絡數字時代的一則精準寓言。

從『BillyBudd』，卡夫卡的『TheTrial』，到奧威爾的『1984』，到著名黑客KevinMitnick寫的超級大賣書『隱形的藝術』，似乎，危機四伏，風險不斷累積，對末日世界的想象給了作家們很好的素材……

偶爾無意中看到了一本有趣的漫畫『ThePrivateEye』，它描述了一個劫后余生的后現代場景：在未來，我們的所有信息數據都存放在云上，然后突然有一天，這個數據云「爆炸」了，不知道是什么原因，反正所有的信息，包括每個人最陰暗的過去，都不再成為秘密；所有的數字化的資產都被抹掉，所有的在線知識庫永久丟失；每個人的言行、賬單、郵件、聊天消息、銀行卡密碼、中學考卷、GPS位置信息，寫了一半的日記、刪除的照片、上網記錄，這些信息都將暴露給同事、鄰居、朋友、親人、甚至任何一個好奇的人。

每個人都無地自容，惶惶不可終日，然后逐漸地，大家都選擇隱藏自己，人們出門都要戴上面具，以小心翼翼地保護自己的身份，甚至一個人可以選擇使用多個身份，國家法律規定任何偷窺行為都將被嚴懲，獲取信息成為了一種至少無上的權力，照相機需要被嚴格管控，互聯網不再存在，人們通訊又回到了電話亭時代……

這會是人類的終極命運么？

未完待續

本文開頭提到了「隱藏隨機性」并不是必要的，我們來回想下HiddenBits模型。這些HiddenBits并沒有對Prover隱藏，而是敞開了讓Prover知道，但是由于HiddenBits是「一致性隨機分布」的字符串，所以即使讓Prover知道了，他仍然逃不過隨機挑戰的火力。然而在流行的zkSNARK方案中，并沒有采用「一致性隨機分布」的CRS，而是一組結構化的隨機數。不管怎樣，用CRS來構建「信任根基」的秘密，就是藏在其中的「秘密」。

這符合直覺，保守「秘密」也是一種信任。因為Alice不知道CRS中隱藏的秘密后門，所以無法作弊。同樣，Bob不知道CRS中的秘密，也就沒辦法獲得「知識」。同樣，人與人之間的協作既要建立在公開透明的基礎上，也要保守秘密。

Allhumanbeingshavethreelives:public,private,andsecret.每個人都有三種生活，公開的，私人的，以及秘密的。——GabrielGarcíaMárqueel

致謝：感謝陳宇，丁晟超，張宇鵬，胡紅鋼，劉巍然，何德彪，萬志國等老師的專業建議和指正，感謝安比實驗室小伙伴的修改建議。本文內容不代表他們觀點。

最后附上漫畫書的鏈接：http://panelsyndicate.com/comics/tpeye作者甚至把創作過程的郵件和草圖都放了出來，大家可以體驗一下窺視制作過程的快感。

參考文獻

Aaronson,Scott.Reasonstobelieve,2006.https://www.scottaaronson.com/blog/?p=122

Blum,Manuel,PaulFeldman,andSilvioMicali."Non-interactivezero-knowledgeanditsapplications."STOC'88.1988.

Bellare,Mihir,andShafiGoldwasser."Newparadigmsfordigitalsignaturesandmessageauthenticationbasedonnon-interactivezeroknowledgeproofs."ConferenceontheTheoryandApplicationofCryptology.Springer,NewYork,NY,1989.

Boneh,Dan,Eu-JinGoh,andKobbiNissim."Evaluating2-DNFformulasonciphertexts."TheoryofCryptographyConference.Springer,Berlin,Heidelberg,2005.

Brakerski,Zvika,ShafiGoldwasser,GuyN.Rothblum,andVinodVaikuntanathan."Weakverifiablerandomfunctions."InTheoryofCryptographyConference,pp.558-576.Springer,Berlin,Heidelberg,2009.

Bellare,Mihir,andMotiYung."Certifyingpermutations:Noninteractivezero-knowledgebasedonanytrapdoorpermutation."JournalofCryptology9.3(1996):149-166.

Canetti,Ran,ShaiHalevi,andJonathanKatz."Aforward-securepublic-keyencryptionscheme."InternationalConferenceontheTheoryandApplicationsofCryptographicTechniques.Springer,Berlin,Heidelberg,2003.

Chiesa,Alessandro,etal.Marlin:Preprocessingzksnarkswithuniversalandupdatablesrs.CryptologyePrintArchive,Report2019/1047,2019,https://eprint.iacr.org/2019/1047,2019.

Dwork,Cynthia,andMoniNaor."Zapsandtheirapplications."Proceedings41stAnnualSymposiumonFoundationsofComputerScience.IEEE,2000.

Feige,Uriel,DrorLapidot,andAdiShamir."Multiplenon-interactivezeroknowledgeproofsbasedonasinglerandomstring."Proceedings31stAnnualSymposiumonFoundationsofComputerScience.IEEE,1990.

Fortnow,Lance."WhatifP=NP?".2004.https://blog.computationalcomplexity.org/2004/05/what-if-p-np.html

Fortnow,Lance."ThestatusofthePversusNPproblem."CommunicationsoftheACM52.9(2009):78-86.

Groth,Jens."Shortnon-interactivezero-knowledgeproofs."InternationalConferenceontheTheoryandApplicationofCryptologyandInformationSecurity.Springer,Berlin,Heidelberg,2010.

Groth,Jens."Shortpairing-basednon-interactivezero-knowledgearguments."InternationalConferenceontheTheoryandApplicationofCryptologyandInformationSecurity.Springer,Berlin,Heidelberg,2010.

Groth,Jens,RafailOstrovsky,andAmitSahai."Perfectnon-interactivezeroknowledgeforNP."AnnualInternationalConferenceontheTheoryandApplicationsofCryptographicTechniques.Springer,Berlin,Heidelberg,2006.

Gabizon,Ariel,ZacharyJ.Williamson,andOanaCiobotaru.PLONK:PermutationsoverLagrange-basesforOecumenicalNoninteractiveargumentsofKnowledge.CryptologyePrintArchive,Report2019/953,2019.

Kilian,Joe,andErezPetrank."Anefficientnoninteractivezero-knowledgeproofsystemforNPwithgeneralassumptions."JournalofCryptology11.1(1998):1-27.

Maller,Mary,etal."Sonic:Zero-KnowledgeSNARKsfromLinear-SizeUniversalandUpdateableStructuredReferenceStrings."IACRCryptologyePrintArchive2019(2019):99.

RanCanettiandAmitLichtenberg."Certifyingtrapdoorpermutations,revisited."TheoryofCryptographyConference.Springer,Cham,2018.

Gasarch,WilliamI."GuestColumn:TheThirdP=?NPPoll."ACMSIGACTNews50.1(2019):38-59.

Yao,AndrewC."Theoryandapplicationoftrapdoorfunctions."23rdAnnualSymposiumonFoundationsofComputerScience(sfcs1982).IEEE,1982.

Tags：LICICEALIALICEHyperbolic ProtocolViceTokenGALIalice幣還有長期價值嗎

芝麻開門交易所下載