比特幣:分析 | 適用于傳統金融衍生品定價的Black-Scholes模型也適用于比特幣嗎？

金融世界動蕩、混亂，無序可循。以至于許多經濟學家都認為市場變化是“隨機游走”的，價格是無法預測的，但是這并不一定就是一件壞事。

在這里我們引入高斯隨機游走的概念，它是Black-Scholes的期權定價模型所使用的基礎假設。這一期權定價模型將資產價格變化的時間間隔視為獨立變量，同時假定價格或資產收益隨時間的變化服從正態分布，換句話說，交易在各個時間段都均勻分布，每天、每周或每月的交易量龐大，因此根據中心極限定理，這些價格將符合正態分布或高斯分布。當資產的收益分布是正態分布時，不同收益情況出現的概率是已知的。了解這些概率可以為投資者提供一個思路，更好地量化持有這些資產時可能出現的風險。

在這個基礎上，我們不禁思考，這一模型是否能應用在比特幣這一新型資產上呢？比特幣的大漲大跌是一個眾所周知的事實，這里不做爭辯。本文旨在探討如何構建風險框架，檢驗傳統金融衍生品定價中隱含的假設在比特幣中的應用情況。

本文最開始將介紹衍生品市場，概述Black-Scholes模型，論述模型的重要性及應用范圍，并根據模型的假設前提中不切實際的地方分析其局限性，討論它應用在比特幣市場的可行性。根據2016年1月至2019年8月期間比特幣日回報率的等歷史數據，我們比較了Black-Scholes模型分別應用于比特幣和標準普爾500指數的結果。最后得出“Black-Scholes模型可能不適用于加密貨幣市場”的結論，并從這一結論中得到對快速增長的代幣衍生品市場的一些啟示。

衍生工具與對沖風險

假設你是一個種植玉米的農民，你希望能收獲5000蒲式耳的玉米，并盡可能多地將它們賣出。然而，價格受市場的供需情況影響，玉米賣出價有低于生產成本的可能，而應用金融衍生品可以將這些情況下造成的損失最小化。

假設目前玉米的市價在每蒲式耳3.50美元左右，而你想“鎖定”3美元的價格下限，那么你可以在3美元的價位買入看跌期權，避免價格跌至3美元以下的可能性。由于看跌期權的價值隨著標的物價格的下降而增加，購買期權的價格就是這次對沖的成本。如果履約價為3美元的看跌期權的成本是10美分(5000蒲式耳*0.10美元=500美元)，玉米的生產成本是每蒲式耳1美元，那么最低利潤為9500美元。

以上示例解釋了金融衍生品的作用。當然，當把全套期貨、期權、掉期等都納入考慮范圍時，這一衍生品投資組合可以變得更加復雜。這些所有的投資組合的基礎都是:市場和價格反映風險和不確定性，衍生品將盡量降低這種不確定性。

有了這個基本理解，我們對任何衍生產品的價格都有一個特殊的考量。衍生品發揮作用的前提是它能夠代表對標的物不確定性的實際對沖，如何應用期權進行有效的投資是一個值得思考的問題。

期權的實際風險其實在標的物的實際價格中就得到了反映。在上面舉的例子中，如果看跌期權的價格是2美元，而不是10美分，而玉米價格還是3.5美元。那么通過Black-Scholes模型可以計算得出此時的玉米價格的波動率高于200%(見附注)，這個數字對于農業市場來說是不同尋常的，基于此，你對玉米的未來價格的預期也會發生變化。第二，就算你的預期不變，以2美元購買看跌期權將大大降低利潤空間，如果玉米價格跌至3美元以下，那么你將會因為期權費的原因產生虧損。第三，如果你的預期發生了變化，同時玉米價格的隱含波動率是可信的，那么以每蒲式耳1美元的成本生產玉米的話，虧損的風險會變得很大。因此，期權定價的有效性至關重要，它反映了市場對未來的預期。

Black-Scholes模型

期權合約的定價過程其實是相當機械的。眾所周知，Black-Scholes模型對期權定價與對沖有著非常重要的作用，同時投資者和交易所也使用這一模型來確定希臘值或計算期權和其他投資組合中的δ，Vega，θ，γ等偏導數。這些偏導數對于交易所/券商所的風險管理有很大的幫助，它們是度量衍生品價格敏感性的系數。舉個例子，當大型加密衍生品交易所Deribit在清算高風險頭寸時，他們的風險引擎實際上是在創建一個“”的對沖倉位，讓delta正負相消，使組合價值不受標的資產價格變動影響。

分析 | ETH周線上升三角整理 中長線多頭趨勢:分析師K神表示：周線級別，自2018年12月跌至熊市最低82美元至當前近1年的時間里，整體走勢結構處于一個大的上升三角區間內震蕩上行，19年的這波小牛行情，最高剛好向上反彈至前期周線M頂頸線位附近，頸線位聚集了大量的前期套牢盤與近期獲利盤，不足的是反彈量能未持續放大，周線收出上插針形態后迅速回落，一路下探至三角下邊線附近止跌企穩，然后這幾周沿趨勢線緩步上行，上漲結構完好并未破位，周線MACD紅柱縮短接近0軸，快慢線有水下金叉趨勢，量能看這段時間上漲放量，回調縮量，大方向看有在三角下邊線筑底蓄勢的跡象，后續在ETH 2.0的推動下，有望變盤向上沖擊上邊線阻力，對于中長線逢低布局為主, 支撐165美金，壓力185美金。[2019/11/20]

自1973年Black-Scholes模型首次在經濟雜志(JournalofpoLiticalEconomy)發表之后，芝加哥期權交易所(ChicagoBoardOptionsExchange，簡稱CBOE)的交易商們馬上意識到它的重要性，很快將模型程序化并應用到剛剛營業的CBOE上，后于1986年推出應用Black-Scholes模型的首個“自動報價”系統(該系統能即時為交易員更新正在交易的期權價格)。可以說，該模型在現代金融的發展，以及增強金融衍生品對市場的影響力上，做出了里程碑式的貢獻。

Black-Scholes模型在加密市場上也造成了影響。最近，比特幣衍生品交易所LedgerX?和SeedCX宣布測試推出以實物結算的比特幣衍生品，任何美國居民都可以參與交易真實的比特幣衍生品，讓許多人對此產生了濃厚的興趣。

這些新的衍生品交易所上市的消息不禁引發了我們的思考：在比特幣的風險管理中，Black-Scholes模型能發揮作用嗎？如果能的話，這個作用有多大？

Black-Scholes模型隱含了對資產收益的假設，即收益率都是服從正態分布的，它提供了一個框架來預測不同收益出現的概率，投資者可以在做套期保值策略中將這一概率作為參考。Black和Scholes在他們最初的論文《期權和公司負債的定價》中指出，這種假設是“股票的價格在連續時間內隨機游走，其方差與股票價格的平方成正比。因此在任何有限區間內股票價格呈對數分布，股票收益率的變化率是恒定的“。這個假設可以通過Black-Scholes公式來說明：

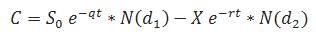
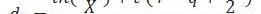
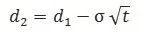
其中：

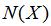
是正態分布變量的累積概率分布函數，表示“價值”的部分。在模型最初的概念中，“價值”部分被表示為股票價格乘以

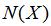
函數。后來，羅伯特·默頓(Robert·Merton)擴展了原模型的內涵，使之同樣運用于許多其它形式的金融交易。

總的來說，Black-Scholes公式的表示投資回報

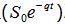
減去購買期權的成本。

分析 | ETH連續5天收陽，或標志著7至8月期間看跌趨勢的逆轉:9月14日至9月18日，ETH連續5天收陽，創下自5月底以來的最長上漲時間段。5月23日至5月27日，ETH也連續5天小幅上漲，這一上漲趨勢加速了自4月2日（當時ETH價格約為140美元）開始的牛市。隨后ETH在6月26日達到364美元的高位，然后在8月底收至167美元。最近五天的漲勢得益于ETH交易量的上升，并標志著7至8月期間看跌趨勢的逆轉。因此，有充分的理由相信在目前的回調可能是短暫的。（Coindesk）[2019/9/19]

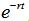
用來解釋無風險利率，它從購買至期權到期的期間連續復利。本質上來說，

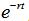
表示“貨幣的時間價值”，它是期權執行價格

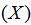
的現值，在理想情況下的期權價值應該高于目前國債(T-bill)或政府債券的無風險利率，因為如果投資者能通過購買國債獲得更高的收益，那就沒有購買期權的意義了。

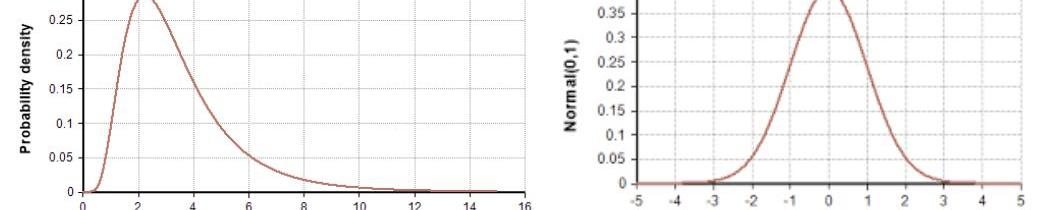
圖1：對數正態分布(左)與正態分布(右)

還有一點是，Black-Scholes模型中期權價格的分布是對數正態分布。由于對數正態分布的下限為0，而資產價格不可能是負的，因此假設其價格服從對數正態分布。

期權到期時

是正態分布的，這意味著價格的分布是傾斜的，因此平均數、中位數、眾數這三者是不相等的。

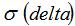
代表資產價格的日波動率。收益

除以日波動率的標準差

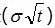
為正態分布。在收益呈正態分布的情況下，資產的波動率

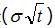
用函數

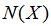
加權將確定分布曲線。由于波動率是按

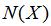
加權的，所以

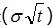
的值越高，曲線越“平”。

分析 | 量能衰減至5500附近橫盤震蕩水平 BTC大概才會選擇方向突破:4小時走勢看，BTC仍處于箱體區間7500美元至前高8360美元上下震蕩，同時也處于上升楔形三角區間內震蕩上行，量能逐漸衰減，MACD有即將死叉趨勢，短期仍有下探的風險，但在未明確出現選擇方向突破之前，整體依然延續區間震蕩行情。周線走勢BTC依舊受制于18年波段高點8400美元的壓制，從站上8000美元上方以來多次刺探一直未能形成有效突破，后續若能放量站穩該點位上方，盤面看下一真正阻力區在9500美元上方，若一直不能有效突破幣價拐頭向下，周線級別支撐在7300美元附近。近期在未出現方向選擇突破之前，操作上仍以區間7800至8200高拋低吸為主，估計后期量能繼續處于萎縮趨勢，預計萎縮到3周前BTC在5500美元附近橫盤震蕩時的縮量水平，波動也將收斂到極致，BTC才會啟動大的方向選擇突破。[2019/5/26]

圖2：期權執行價格概率分布

當函數

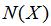
為

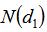
時，該函數表示期權在到期日時標的價格高于行權價格的概率。我們可以通過圖2來描述這個問題，在看漲期權的情況下，如果用“a”表示行權價格，

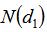
表示標的價格增加的時候期權的期望值。當標的資產價格小于a時,不行權，

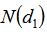
視為0，即看漲期權的價值為0。而當“a”表示看跌期權的執行價格時，標的價格大于a時看跌期權的值為0。

另一方面，

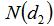
表示在風險中性測度下，期權被執行的可能性。這里可以再次利用圖2來說明：假設a表示行權價格，在看漲期權里

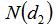
表示標的價格高于行權價格a的概率；在看跌期權里，

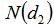
表示標的價格低于行權價格a的概率。

在連續復利情況下，通過限定標的資產價格呈幾何布朗運動，Black-Scholes模型其實就是限定了標的資產收益率必須呈正態分布。通過模擬資產增長率的概率來確定資產價格高于或低于給定的行權價格的概率，即計算從股票價格到行權價格的增長率與預期增長率之間的標準差

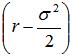
從而確定增長率。總的來說，只有當標的價格大于行權價格時(對于看漲期權，此時概率為

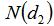
，才會行權，在風險中性的世界中，該期權的預期收益是：

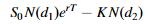
而波動率越高，正態分布曲線的面積就越大，期權價格越高。因此，期權價格可以被認為是一個概率分布。

分析 | 英國脫歐進程造成了此次數字貨幣的波動:據ethereumworldnews文章分析，在英國決定推遲脫歐后，數字貨幣市場出現了整體的下滑。而在此之前，由于脫歐的影響，導致人們對歐元和英鎊的信心出現下降，分析人士開始呼吁用數字貨幣抵御這種風險。但在英國推遲脫歐后，歐元和英鎊將暫時安全。不過分析師也指出，當前的下跌很可能只是正常的回調。[2019/4/12]

假如波動率非常穩定，并且某只股票在期權到期時100%會高于看漲期權的行權價格或100%低于看跌期權的行權價格，那么這個期權就沒有價值了。實際上，從套期保值的角度來看，此時選擇期權是沒有意義的，因為沒有風險需要對沖。或者假設股票在期權到期時有50%的可能性會高于看漲期權額行權價格或有50%的可能性低于看跌期權的行權價格，那么這個期權是有價值的，因為它能夠吸引投資者購買期權，以對沖持有基礎股票的風險。

Black-Scholes模型的缺陷

Black-Scholes模型絕不是完美的。某種程度上來說，Black-Scholes模型對市場的假設與實際情況不相符。通過這一模型，交易者只需輸入行權價、到期剩余時間、標的資產價格、標的資產波動率和無風險利率等參數便可得到相應的期權價格。

上述參數中，有四個參量的值都可以從市場上準確的獲得，只有標的資產價格波動率需要估計。而該模型假設波動性不僅是常數，而且可以預先知道。這種假設存在問題，因為波動性本身可能是不穩定的。CBOE創建了恐慌指數(VIX)，指的是S&P500指數未來30天的隱含波動率。2018年，恐慌指數(VIX)最低跌至8.5%，最高超過46%。因此全年的波動性并不總是一致的。

Black-Scholes模型的準確性同時也會因為市場的變化而受到影響。1987年金融市場崩潰，衍生產品市場也同時受到影響。在1987年之前，隱含波動率與執行價格之間沒有太大關系，價外看跌期權和價內看漲期權的波動率基本相同。然而，在1987年出現了讓人毛骨悚然的“波動率微笑(Volatilitysmiles)”，如圖3所示，當期權現價與行權價格偏離時，期權的隱含波動率上升，從而呈現出中間低兩邊高的微笑的嘴形。對于不同的金融期權而言，隱含波動率的形狀也不盡相同，一般來說股票期權的波動率曲線可能會出現歪斜，被稱為波動率偏斜。

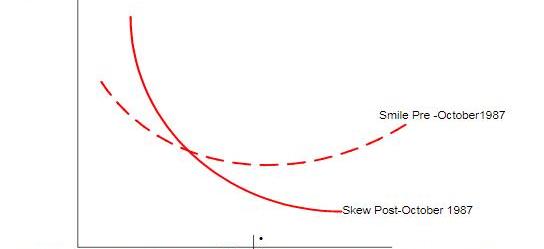
圖3：CBOE偏斜指數

這種偏斜可以表示市場的恐慌。如果一個看跌期權隱含波動率遠高于看漲期權，這可以解釋為投資者對規避下行風險所做的套期保值的比例不為一。

在圖3的例子中，圖表表明標準普爾500指數呈現負波動率偏斜的現象。一個原因是越來越多的投資者喜歡買入股票價內看漲期權而不是直接買入股票，因為買入期權可以帶來杠桿效應，即付出相當于股價金額一部分的期權費即可享有股價同等漲幅的好處，而買入股票需要占用相當于百分之百股價的資金。這樣做的結果是投資者的回報率會得以提升，因此市場對股票價內看漲期權的需求出現增加，并導致較低行權價的看漲期權的隱含波動率水平上行。

因此，盡管Black-Scholes模型的正態分布曲線在兩端給出的概率相等，但實際上股票期權市場往往表現得更為悲觀。而有趣的是，相較而言下的比特幣市場的樂觀程度要高得多。

圖4：到期日為2019年12月27日的比特幣期權表

圖4顯示了比特幣期權平臺Deribit于2019年12月27日到期的比特幣衍生品。可以看出與比特幣現價(10000+)偏離程度相同的兩個價格(7，000和13000)顯示出不同的隱含波動率：在7000點買入的看跌期權的隱含波動率為86.6%，而13000點的看漲期權(左側)的IV略高，為90.2%。這表明，價外看跌期權的價值遠遠低于價外看漲期權，雖然這張期權表并不能代表整個比特幣期權市場，但也說明有相當一部分投機者/投資者低估了下行風險。

分析 | 金色盤面：USDT 場外交易數據:金色盤面綜合分析：USDT/CNY價格6.93，創出8月2日以來新高，USDT價格走高，短期需求增加所致，這主要是避險情緒提高，資金從數字貨幣市場流出，對BTC價格構成壓力。[2018/8/9]

因此Black-Scholes模型并不能被神化，相反的是，在使用這一模型來定價期權時，應該保留懷疑的態度。正如上文所指出的，Black-Scholes模型仍然被廣泛使用，它更多提供的是一個基準，交易者可以快速發現期權價格的相對貴賤，但同時一些平臺對這種易于應用的模型產生了過度依賴。

峰度的不可預測性

峰度是數據分布的平坦度。尾部大的數據分布，其峰度值較大，反映了未來尾部的風險特征。樣本超額峰度公式為：

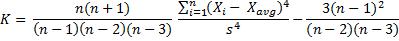
其中：

峰度為：

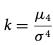
在計算資產收益分布的峰度時，偏離均值(每個隨機變量之間的差額)X和所有值的平均值)每日收益是必要的。這種偏離可以表示為：

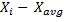
在統計學里，矩描述的是概率分布的形狀。一般來說，一階距和二階矩分別表示分布的均值和方差，三階矩代表偏度(Skewness)。如前所述，偏度用來衡量分布不對稱或者傾斜的程度。四階距反映分布的尖峭程度，并以不同的方式改變正態分布的曲線。可以表示為：

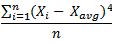
為了消除變量值水平和計量單位不同的影響，實際工作中是利用四階中心矩

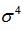
與的比值作為衡量峰度的指標，稱為峰度系數。計算峰度時，通常假定超額峰度已被考慮在內。正態分布的峰度為3，如圖5所示，如果一個分布的峰度大于3，則稱為正峰度（尖峰leptokurtic)，從形態上看，相比于正態分布更陡峭或尾部更厚，也就是均值兩邊的值變化的范圍將大于正態分布，這意味著，資產價格將變得更加不可預測的，因為價格劇烈波動的概率增加了；當峰度小于3時，負峰度（扁峰playkurtic)，從形態上看，相比于正態分布更平緩或尾部更薄。

在計算超額峰度時，該公式為：超額峰度=峰度-3。當一項資產出現超額峰度時，持有該資產的內在風險就會更大。

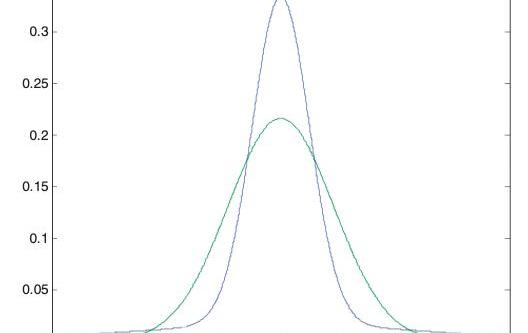
圖5：方差相同的正態分布與正峰度的形狀

峰度可以用來衡量風險，在這里我們暫時忽略“隨機游走”這樣的基本假設。在任何給定的時間框架內找出收益率的峰度，可以讓投資者了解波動性是如何分布的。資產回報的正態分布與否可以描述不同的風險情況。投資界大多數人選擇將波動性和風險視為一回事，認為資產波動性越大，風險就越大。反之，資產波動性越小，則越安全。然而，這種波動/風險的二元論忽略了波動的性質，甚至將具有正態分布的收益歸到“風險”類別。

我們限定收益服從正態分布時，那么不同收益情況的概率是可知的。例如，假設某一資產的收益的正態分布邊緣達到-50%和50%，這種資產將被認為是極不穩定的，但如果該收益是服從正態分布的，那么可以得出該曲線的尾部和邊緣與平均值相比分別有2和3個標準差。一旦知道了這些信息，投資策略就可以圍繞這種可能性進行調整，甚至非常不穩定的資產也可以像波動較小的資產一樣進行交易。因此，與其把風險和波動性混為一談，不如讓它們建立正交關系，這種關系可以作為波動風險指南針。

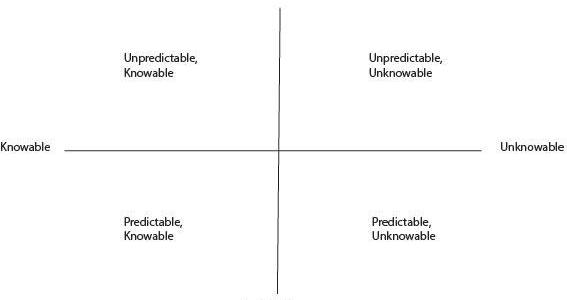
圖6：波動與風險的正交關系

在圖6中，假設縱軸為價格的可預測程度，橫軸為收益的概率分布的可知程度。在這張圖中，上象限為不可預測的價格，代表“隨機游走”；左象限為收益率的概率分布已知，代表收益服從正態分布。

在圖7中，左上角表示基于“理想”假設的Black-Scholes模型中的資產。這樣的資產經過“隨機游走”，價格是不可預測的，而收益率是正態分布的，因此概率分布是可知的。而右下角代表Black-Scholes模型的對立面，資產的價格可預測，但概率分布不可知，這種資產可以被認為是被操縱的，無論是通過內幕交易還是一般情況下的技術分析，價格都是完全可以預測的，但出現的概率不定。隨著時間的推移，這種資產的價格可以被完全操控，則沒有了預測收益率的概率分布的必要。而左下角的價格可預測，其概率也可知。這樣的資產可以被認為是“穩定的”，不應該有任何的價格偏差，未來收益率也可知。最后，右上角代表的是遵循“隨機游走”的資產，但其收益概率的分布不正常。

圖7：波動率-風險指南針

有了波動率-風險指南針，就可以刻畫更清晰的圖像來明確一項資產的風險情況。在此基礎上，峰度可以用來確定某資產落入哪個象限。資產的峰度量化了期權的風險，因為超額峰度意味著由Black-Scholes模型的定價不一定可靠。

此外，在研究“風險調整后的收益情況”時，找到投資組合中資產的峰度可以更準確地衡量投資組合的價值。這是因為峰度可以衡量投資組合的“尾部風險”。通過識別“尾部風險”而不僅僅是考慮波動性，投資者可以更好地明確其投資組合中的風險。因此，在試圖解釋比特幣所存在的風險時，僅僅關注比特幣的波動性是不夠的。假設其收益率服從正態分布，那么就可以給出比特幣期權的準確價格，從而量化風險。而如果收益率不服從正態分布，那么期權價格上的收益分布概率就變得不那么具有參考意義了。

比特幣峰度

通過觀察2016年至2019年8月比特幣的日收益率(數據來源：coinmarketcap)，就可以得到比特幣的超額峰度。自2016年1月以來，比特幣出現了超額峰度。

圖8：比特幣每日收益2016年(左)、2017年(中)、2018年(右)

圖8顯示了2016年、2017年和2018年比特幣日收益的分布情況，并根據數據繪制了正態分布曲線。從圖表中可以清楚地看出，比特幣并不遵循正態分布。而將圖8與圖5進行比較，我們可以發現比特幣更像是一個正峰度。在計算2016年、2017年和2018年的超額峰度后，可得每個圖表的日收益率范圍從-20.00%到20.00%。但在2017年，有兩個觀測結果超出了這一范圍。對于比特幣來說，2017年是一個特別不穩定的年份。到了2018年比特幣波動性略有下降，但仍存在顯著的“尾部風險”。值得注意的是，2018年比特幣價格出現了更為劇烈的下跌。

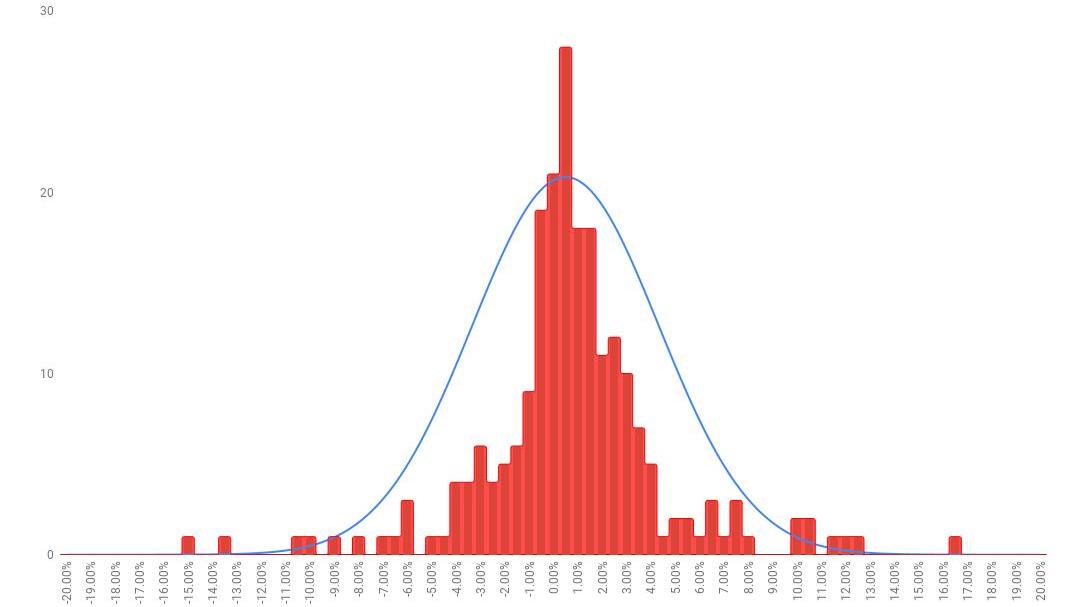
圖9：2019年比特幣每日收益

到目前為止，比特幣的峰度并沒有下降。相反，相較于2018年略有上升，超額峰度為3.92。雖然這一年內的每日收益在接近其平均值的概率分布較大，但其尾部的概率分布相對均勻。這展現了一個經典的正峰度，尾部更厚，均值兩邊的值變化的范圍大于正態分布。

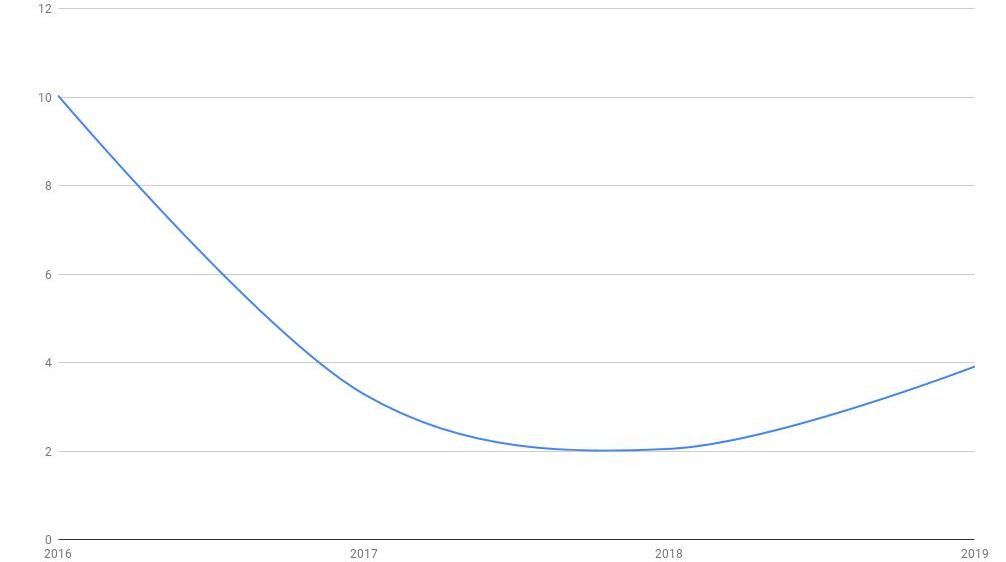
圖10：2016-2019比特幣超額峰度

總體而言，超額峰度顯示，比特幣日收益率的概率偏斜使用Black-Scholes模型得出的平均值和尾部將大于預期。給期權定價可能會變得非常困難，因為隱含波動率變得不那么可靠。超額峰度意味著大部分的價格變化變得不可預測，波動性不服從正態分布。

因此，一項資產可能表現出相對較低的波動率，因而使價格大幅度變化的可能性很低，但這種波動并不能真正代表一項資產的波動性。回顧圖7中的波動率-風險指南針，比特幣很可能是右上角所代表的資產類型。據推測，比特幣的價格是不可預測和隨機游走的，其收益的概率并不服從正態分布。

比較與結論

到目前為止，我們已經證明比特幣表現為超額峰度。那么與更為廣泛討論的股票市場相比，比特幣是一個異常值嗎？也是，也不是。在比特幣之外，還有許多資產也同樣表現出超額峰度，甚至標準普爾500也是如此。2018年，S&P500出現了3.09的超額峰度。低于比特幣2016年、2017年和2019年的超額峰度，但高于2018年。對S&P500而言，2018年是非常不穩定的一年，股市歷經大漲大跌。如圖11所示，2018年初，指數突然下跌超過10%，此時對應相對極端的峰度。

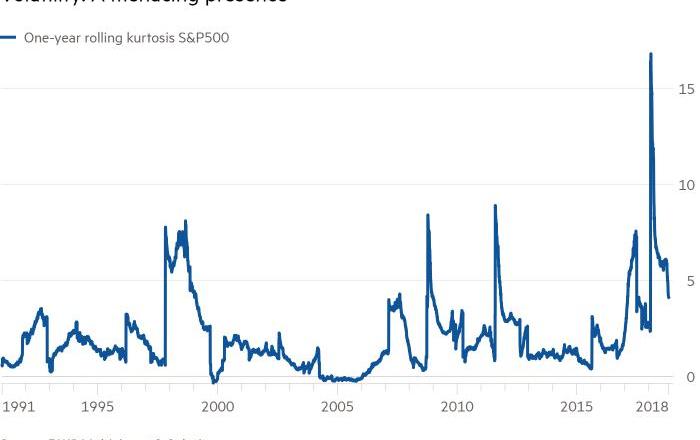
圖11：S&P500峰度變化情況

在圖12的直方圖中顯示，S&P500的日收益率分布，比起比特幣來說更接近正態分布。盡管有部分日收益遠遠超出正態分布曲線，明顯存在超額峰度。但總的來說，S&P500這250個觀察結果中只有6個超出正態分布曲線。而在2017年比特幣日收益率的364次觀察結果中，有28個超出了正態分布曲線。根據數據對比，我們發現S&P500日收益率曲線的下降速度非常快，出現極端價格波動的可能性較低，因此使得人們難以預測到事件的極端變化，波動不可預測。

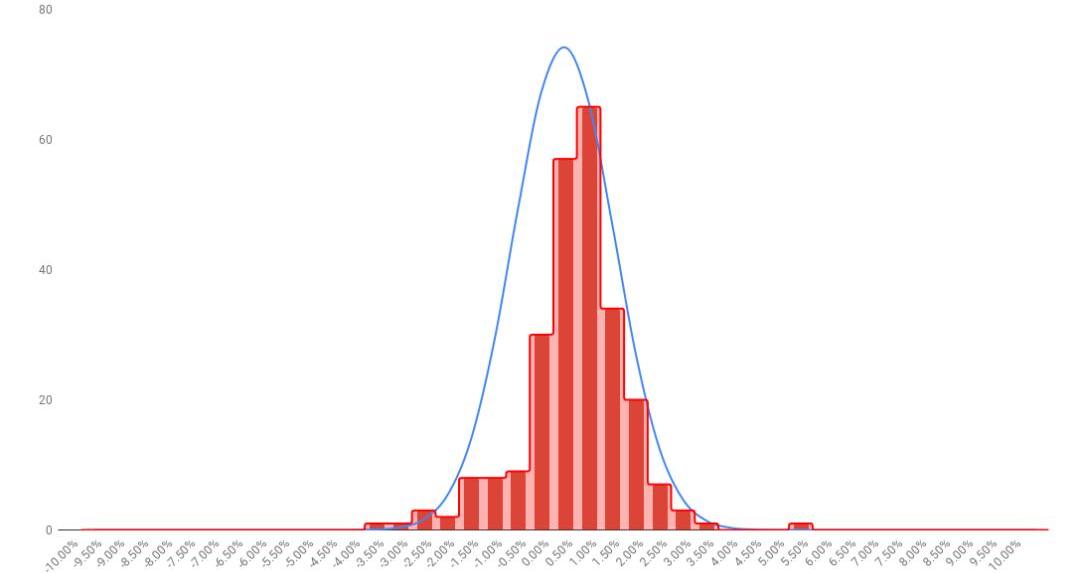
圖12：2018年標準普爾500日收益率

那么我們可以從中得到哪些啟示？雖然標普500指數確實沒有落入正態分布曲線，但它確實比比特幣更符合正態分布的曲線。造成這個結果的具體原因還有待推敲，但我認為至少有三個可能。首先，比起廣泛的股票市場而言，比特幣代表著不同的資產類別，并遵循不同的基本假設。其次，目前的比特幣市場仍不成熟，缺少專門的投資機構的管控。第三，總的來說Black-Scholes模型的可靠程度存疑，波動的不可預測成為“新常態”。

不管是這些原因中哪一個，我們都可以得出結論：在這種情況下，比特幣期權定價模型很有可能出現錯誤，比特幣投資組合的“三角套利”估值也不準確。尤其是在許多新的加密貨幣衍生品交易所爭先上市的情況下，后期可能會導致更多問題的出現，因為比特幣相對較高的隱含波動性和這種波動率背后隱藏著的超額峰度，將使投資者規避風險的能力大大降低，不能夠量化風險。

附注

從Brenner和Subrahmanyan的“計算隱含標準差的簡單公式”和Black-Scholes模型中我們可以得到：

其中：

在我們一開始舉的玉米的例子中，期權價格為2美元，玉米當前價格為3.5美元，并假定期權合約為期6個月。這里值得注意的是，上述公式是計算看漲期權價格的波動率。而這個玉米示例是一個看跌期權。因此，根據這個公式就算出的波動率將略有不準確。然而，為了簡單起見，我們把這個期權當作了一個看漲期權。

使用上述公式得到：

σ=√(2π/5)*(2/3.5)

σ=202.73%

來源：Brenner,MenachemandMartiSubrahmanyan,“ASimpleFormulatoComputetheImpliedStandardDeviation.”FinancialAnalystsJournal44(5)(1988).81

參考資料

Black,Fischer&MyronScholes.“ThePricingofOptionsandCorporateLiabilities.”JournalofPoliticalEconomy81(3)(1973).

Fama,EugeneF.“EfficientCapitalMarkets:AreviewofTheoryandEmpiricalWork.”TheJournalofFinance25(2)(1970).

Hull,JohnC.Options,Futures,andOtherDerivatives.TenthEdition.NewYork:PearsonEducation,(2018).

MacKenzie,Donald.AnEngine,NotaCamera.Cambridge,MA:MITPress,2006.

McAlevey,LynnG.andAlanF.Stent.“Kurtosis:aForgottenMoment.”InternationalJournalofMathematicalEducationinScienceandTechnology49(1)?(2017).

Malkiel,BurtonG.“TheEfficientMarketHypothesisandItsCritics.”JournalofEconomicPerspectives17(1)(2003).

Westfall,PeterH.“KurtosisasPeakedness,1905–2014.R.I.P.”AmStat68(3)(2014).

文章來源：哈希派

原文：KurtosisandBitcoin:AQuantitativeAnalysis

譯者：Adeline

Tags：比特幣SCHACKHOL比特幣價格今日行情狗狗幣Synth sCHFPACKTHOL價格

LTC